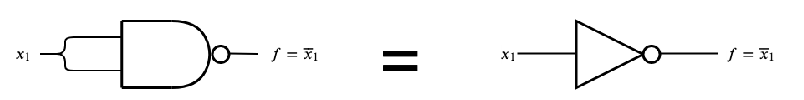09_Algebra-booleana

Questo file è la rielaborazione delle slide 09_Algebra-booleana.pdf

---

Operatori logici

l’algebra booleana della commutazione è un sistema algebrico in cui ogni variabile può assumere solo 2 valori (0 o 1). Possiede $3$ operazioni basilari:

• Somma logica o OR
  • ovvero una funzione che accetta 2 argomenti è vale 1 solo se almeno uno dei suoi ingressi è 1. Si denota tramite gli operatori a due argomenti “+” o “V”.
  • Di seguito le proprietà:
    • Commutativa: $x_1+x_2$ = $x_2+x_1$
    • Associativa: $x_1+(x_1+x_2)=(x_1+x_2)+x_3$
    • Elemento neutro: $0+x=x$
• Prodotto logico o AND
  • Una funzione che accetta 2 argomenti in input e vale 1 solo se tutti i suoi ingressi sono 1. Si denota tramite gli operatori a due argomenti “·” o “∧”
  • Di seguito le proprietà: - Commutativa: $x_1\cdot x_2$ = $x_2\cdot x_1$ - Associativa: $x_1\cdot (x_1\cdot x_2)=(x_1\cdot x_2)\cdot x_3$ - Elemento neutro: $1\cdot x=x$
• Complementazione o NOT
  • è una funzione che accetta un’argomento e ne inverte il valore. Si denota tramite l’operatore di sopra lineatura “¯” o di negazione “¬” Di seguito la tabella di verità di tutte le espressioni 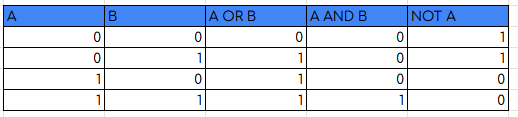OR (somma) e AND (prodotto) hanno le seguenti proprietà:

---

Varie definizioni

Funzione logica: definiamo funzione logica una funzione con più variabili binarie di ingresso ed una variabile binaria di uscita.

---

Tabella di verità: tutte le funzioni logiche possono essere espresse attraverso una tavola di verità, queste tabelle sono formate da $2^n$ righe ed $n+1$ colonne, dove $n$ è il numero di variabili in ingresso.

---

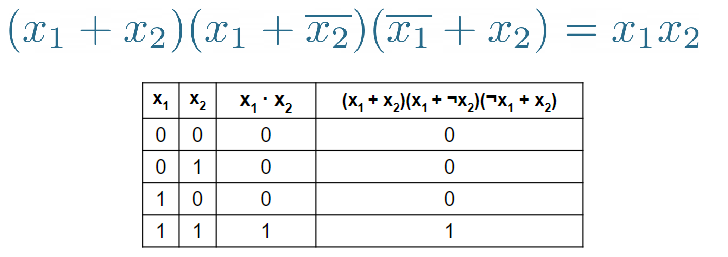
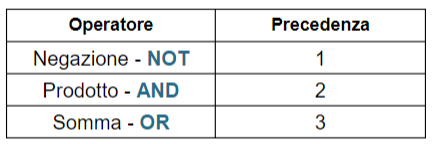
Espressioni logiche: Unendo più funzioni logiche si ottengono le espressioni logiche, esistono infinite espressioni logiche che danno come risultato la stessa funzione logica. Due espressioni logiche si dicono equivalenti se rappresentano la stessa funzione logica, come nell’esempio di seguito: Nel risolvere un’espressione logica dobbiamo stare attenti alla precedenza tra gli operatori, di seguito gli ordini di precedenza da seguire:

TIP

Per calcolare i valori assunti da una funzione ci basta calcolare la sua tabella di verità

---

Mintermine: funzione ad $n$ variabili che vale $1$ solo per una specifica configurazione delle variabili.

---

Maxtermine: funzione ad $n$ variabili che vale 0 solo per una specifica configurazione delle variabili.

---

Forme canoniche: tutte le espressioni logiche possono essere rappresentate in delle forme dette “normali”

---

Forma minima: Un’espressione logica si dice in forma minima quando non esiste nessun’altra espressione equivalente con un costo inferiore, il costo di un’espressione logica è dato dal numero di comparse delle variabili nell’espressione stessa.

---

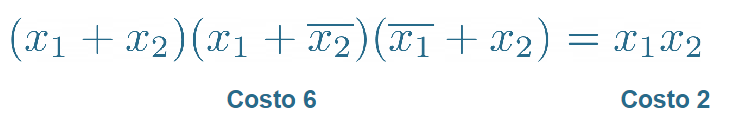
per passare da prima forma canonica a forma minima seguire i seguenti passi:

---

Porte logiche

Tutte le operazioni logiche citate possono essere eseguite da semplici circuiti elettronici, questo circuiti sono formati da delle porte logiche, ognuna va a rappresentare una delle operazioni logiche sopracitate. 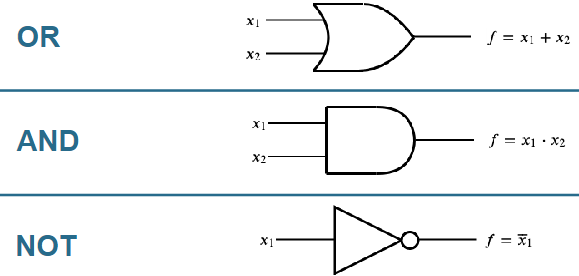Queste porte godono di tutte le proprietà delle funzioni logiche. Inoltre abbiamo anche altre 3 porte molto importanti:

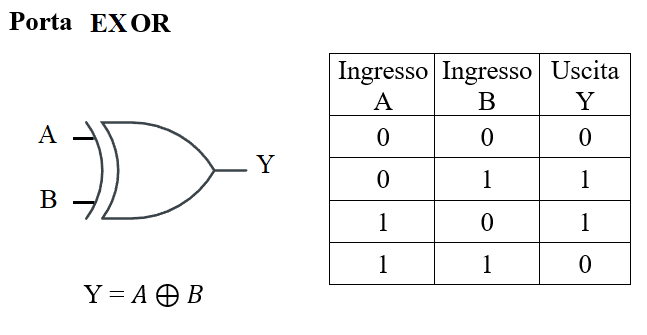
1. XOR (anche detto OR esclusivo): funzione che vale 1 solo se gli 1 nei sono ingressi sono in numero dispari, si denota con il simbolo “⊕”
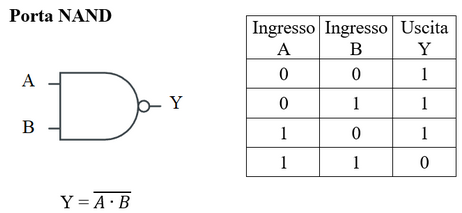
2. NAND: porta che si denota con il simobolo "$\uparrow$" e ha la seguente tabella di verità
3. NOR: porta che si denota con il simbolo "$\downarrow$" e ha la seguente tabella di verità 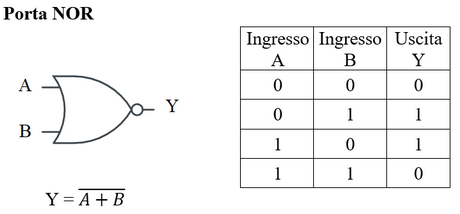Le porte NAND e NOR sono considerate porte universali, usando queste porte si può realizzare qualsiasi funzione.

• una porta NAND con ingressi unificati si comporta come una porta NOT