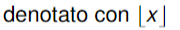02_Parte2

Questo file è la rielaborazione delle slide 02_Parte2.pdf

Numeri interi

Sull’insieme N sono definite 2 operazione:

• Somma: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n+m\in N$
• Prodotto: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n\ast m\in N$ Sull’insieme Z sono definite 3 operazioni:
• Somma e prodotto come definite per N
• Differenza: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n-m$ ∈ Z
• In Z definiamo anche il valore assoluto in questo modo $|n|=\{\begin{array}{ll}n& \text{se }n\ge 0\\ -n& \text{se }n<0\end{array}$ Giuseppe Peano dà una definizione dell’insieme dei numeri naturali in questo modo:
• Esiste un numero naturale 0
• Ogni numero naturale $a$ ha un numero naturale successore denotato come $S(a)$
• Non esiste un numero naturale il cui successore è 0
• Numeri naturali distinti hanno successori distinti

Introducendo la funzione successore (S(a)) è possibile definire una relazione di ordinamento sui numeri naturali, questo viene chiamato assioma del buon ordinamento infatti in un generico insieme S esiste un elemento minimo ovvero esiste un elemento s ∈ S tale che s ≤ t per ogni t ∈ S.

Ricordiamo:

• le proprietà fondamentali della somma sono Commutatività, Associatività e Elemento neutro
• le proprietà fondamentali del prodotto sono Commutatività, Associatività, Distributività, Elemento neutro e Elemento zero
• inoltre il calcolo avviene rispettando le priorità degli operatori

---

Principio di induzione

Peano introduce anche il Principio di Induzione, che afferma: se una proprietà $P$ è valida per il numero $0$ e, ogni volta che è valida per un numero naturale, lo è anche per il suo successore, allora $P$ è valida per tutti i numeri naturali.

Esempio principio di induzione.pdf

---

Floor e Ceiling

Sia x un numero reale, definiamo i 2 seguenti valori:

• “Floor”: il più grande numero intero minore o uguale ad x
  • 
• “Ceiling”: il più piccolo numero intero maggiore o uguale ad x
  • 

Esempi

---

Divisione tra interi

Dati due interi $a,b\in Z$, chiamati rispettivamente dividendo e divisore, esistono unici due interi relativi $q,r$, denominati rispettivamente quoziente e resto, tali che $a=q\cdot b+r$ con $0\le r<|b|$.

Legenda

a = dividendo b = divisore q = quoziente r = resto

In questo tipo di divisione noi abbiamo 4 casi:

• Nel primo caso assumiamo che il dividendo a ed il divisore b siano entrambi non negativi
  • É sempre possibile trovare un unico quoziente $q$ e un unico resto $r$ tali che:
    • $a=qb+r$
    • $q=\frac{a}{b}$ come risultato prendo solo la parte intera
    • $r=a+qb$
    • $0<=r<b$

Esempio

$a=1$, $b=10$: $q=\frac{1}{10}=0$ e $r=\frac{1}{10}\times 10=1$ quindi 1 mod 10 = 1

• Nel secondo caso assumiamo che il dividendo a sia negativo ma il divisore b positivo
  • Assumiamo allora che $a<0$ mentre $b>0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(-q^{\prime })b+(-r^{\prime })$
    • $q=-q^{\prime }-1$
    • $r=b-r^{\prime }$

Esempio

$a=-1$, $b=10$: per $a=1$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per a = -1 abbiamo $q^{\prime }=-1$ e $r^{\prime }=10-1=9$ quindi -1 mod 10 = 9

• Nel terzo caso assumiamo che il dividendo a sia positivo e il divisore b negativo
  • Assumiamo allora che $a>0$ e $b<0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(-q^{\prime })b+(-r^{\prime })$
    • $q=-q^{\prime }$
    • $r=r^{\prime }$

Esempio

$a=1$, $b=-10$: per $b=10$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per b = -10 abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ quindi 1 mod -10 = 1

• Nel quarto caso assumiamo che il dividendo a ed il divisore b siano entrambi negativi
  • Adesso assumiamo che $a<0$ e $b<0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(q^{\prime }+1)b-b-r^{\prime }$
    • $q=-q^{\prime }+1$
    • $r=-b-r^{\prime }$

Esempio

$a=-1$, $b=-10$: per $a=1$ e $b=10$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per $a=-1$ e $b=-10$ abbiamo $q^{\prime }=1$ e $r^{\prime }=10-1=9$ quindi -1 mod -10 = 9

Sommario

Riepilogando, dati due interi $a,b\in Z$ con $b\ne 0$, per trovare quoziente e resto positivo della divisione $\frac{|a|}{|b|}$ agiamo così:

• Troviamo il $q\prime$= $\frac{|a|}{|b|}$ ovvero il massimo intero $q\prime$ tale che $|a|-q\prime |b|\ge 0$ e fissiamo $r\prime =|a|-q\prime |b|$
• Se sia $a$ che $b$ sono positivi poniamo $q=q\prime$ e $r=r\prime$.
• Se $a$ è negativo e $b$ positivo poniamo $q=-q\prime -1$ e $r=b-r\prime$.
• Se $a$ è positivo e $b$ negativo poniamo $q=-q\prime$ e $r=r\prime$.
• Se sia $a$ che $b$ sono negativi poniamo $q=q\prime +1$ e $r=-b-r\prime$.

---

Definizione di divisibilità

Dati 2 interi relativi $n,m\in Z$ si dice che m è un divisore di n se esiste un intero relativo $k\in Z$ tale che n = $k\ast m.$ In altre parole m è un divisore di n se $n$ mod $m$ è uguale a 0, in tal caso useremo la notazione $m|n$. Se m non è un divisore di n quindi $n$ mod $m$ è diverso da 0 usiamo la notazione $m\nmid n$

• un numero $m|2$ si dice pari
• un numero $m\nmid 2$ si dice dispari visto che il resto della sua divisione per 2 è uguale ad 1 esiste un intero k tale che
• $n=2k+1$

---

Dimostrazione per induzione che la somma dei primi n numeri dispari è $n^2$

• Caso base: n = 1 e la somma in questo caso è proprio $1=1^2$
• Caso induttivo: Assumendo che la somma dei primi n-1 numeri dispari è uguale a $(n-1{)}^2$ e un generico numero dispari è definito con: $n=2k+1$, quindi se aggiungiamo a $(n-1{)}^2$ il numero dispari successivo quindi $2(n-1)+1$ otteniamo:
• $(n-1{)}^2+2(n-1)+1=n^2-2n+1+2n-2+1=n^2$

Esempio

$n=5$ $n^2=5^2=25$ $(5-1{)}^2+2(n-1)+1=16+9=25$

---

Proprietà della divisibilità

• Somma: Se $a|b$ e $a|c$ allora $a|(b+c)$
• Prodotto: Se $a|b$ allora $a|bc$.
• Transitività: Se $a|b$ e $b|c$ allora $a|c$
• Quadrato: Se $a|b$ allora $a|b^2$
  • Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, quindi $bc=axc$ questi dimostra che $a|b\ast b$
• Combinazione lineare: Se $a|b$ e $a|c$ allora $a|(hb+kc)$ per ogni $h,k\in Z$
  • Dimostrazione: Se $a|b$ allora $a|hb$, se $a|c$ allora $a|kc$ ovviamente valgono per ogni $h,k\in Z$ e quindi è vero che $a|(hb+kc)$
• Proprietà del numero 0: Ogni $a\in Z$ è divisore di $0$
  • Dimostrazione: $a\in Z$ abbiamo che $a\ast 0=0$ quindi $a|0$
• Antisimmetrica: Siano $a,b\in Z$ se $a|b$ e $b|a$ allora $|a|=|b|$ ossia $a=\pm b$
  • Dalle ipotesi abbiamo che $b=ax$ e $a=by$. Quindi $a=axy$, raccogliendo a arriviamo ad $a(xy-1)$ questo implica che $a$ sia $0$ oppure che $xy=1$ da questo capiamo che:
    • Se $a=0$ allora anche $b=0$ (perché b = 0x)
    • Se $xy=1$ allora $a$ o $b$ sono uguali a $\pm 1$
• Divisori banali: Siano a $\in$ Z allora $\pm a|a$ e $\pm 1|a$
  • Avendo che $a=a\cdot 1$ oppure che $a=(-a)\cdot (-1)$ possiamo affermare che $\pm a|a$
    • Seguendo la definizione capiamo che $a=b\cdot k$ in questo caso $b=\pm a$ il k che soddisfa le nostre equazioni è k = 1
  • Avendo che $a=1\ast a$ possiamo dire che 1 è sempre un divisore di $a$

---

Minimo Comune Multiplo (MCM)

Dati $a,b\in Z$ si chiama minimo comune multiplo fra a e b un terzo intero positivo m che è il più piccolo multiplo sia di $a$ che di $b$, quindi possiamo affermare che $a|m$ e $b|m$

---

Massimo Comune Divisore (MCD)

Dati $a,b\in Z$ si chiama Massimo Comune Divisore un terzo intero $d\in Z$ tale che $d|a$ e $d|b$ cioè $d$ è il più grande divisore comune tra $a$ e $b$.

---

Algoritmo di Euclide

Il metodo migliore per calcolare il massimo comune divisore è l’algoritmo di Euclide, che si basa su questa osservazione siano $a,b\in N$ e sia $b\le a$. Si basa sulla seguente osservazione matematica, che dimostriamo per induzione:

• Caso base: se b = 0 allora il $MCD(a,b)=a$. Questo perché qualsiasi numero è divisibile per sé stesso.
• Passo induttivo: Supponiamo che $a=qb+ra$ , dove $q$ è il quoziente intero della divisione di $a$ per $b$, e $r$ è il resto, con $0\le r<b$ allora $MCD(a,b)$ = $MCD(b,r)$

Se $b|a$ allora la formula si riduce ad $a=qb$ ($q$ sarebbe $\frac{a}{b}$) avendo resto $0$ il calcolo del $MCD$ diventa $MCD(a,b)$ = $MCD(b,0)$ = $b$.

Dimostrazione: Di seguito la dimostrazione che $MCD(a,b)$ = $MCD(b,r)$

• Se $d$ è un divisore di $a$ e $b$ allora esistono $h$ e $k$ tali che $d$ sia un divisore di $r$ (la formula base per calcolare $r$ è $r=a-qb$ )
  • $a=hd$
  • $b=kd$
  • $r=hd-qkd=d(h-qk)$ (essendo che r può essere scritto come $d$ moltiplicato per un intero allora è vero che $d$ è un divisore di $r$ Definizione di divisibilità)
• Se invece $d$ è un divisore di $b$ e di $r$ allora esistono $h$ e $k$ tali che $a$ è un divisore di $m$ (ricordiamo che la formula base per calcolare $a$ è $a=qb+r$):
  • $b=kd$
  • $r=hd$
  • $a=qkd+hd$ = $d(qk+h)$ (essendo che $a$ può essere scritto come $d$ moltiplicato per un intero allora è vero che è un divisore di b Definizione di divisibilità)

TIP

L’algoritmo di Euclide sfrutta il fatto che il MCD di due numeri non cambia sostituendo il numero maggiore con il resto della loro divisione. Ripetendo questo processo iterativamente, si arriva al caso base, in cui uno dei due numeri è 0, e il MCD è dato dal numero rimanente.

Esempio

$x_1=330$ e $x_2=156$ $x_3=330\mathrm{mod}156=18$ $x_4=156\mathrm{mod}18=12$ $x_5=18\mathrm{mod}12=6$ $x_6=12\mathrm{mod}6=0$ Quindi $MCD(330,156)=6$. Da questo capiamo che il minimo comune divisore tra 2 numeri può essere calcolato trovando ripetutamente il modulo tra b ed il resto

Siano $a,b\in N$ allora esistono $h,k\in Z$ tali che $MDC(a,b)=a\ast h+b\ast k$ Questo vuol dire che il MCD tra due numeri si può scrivere come una loro combinazione lineare

Esempio partendo da risultato dell'esempio precedente

$6=18-12$ $=18-(156-8\ast 18)$ $=-156+9\ast 18$ $=-156+9(330-2\ast 156)$ $=-19\ast 156+9\ast 330$

---

Numeri primi e coprimi

Si definisce numero primo un intero che ha come divisori quelli banali ovvero 1 e se stesso. Due numeri $a,b\in Z$ si dicono coprimi se $MCD(a,b)=1$ quindi esistono $h,k\in Z$ tali che $(a\cdot h+b\cdot k)=1$

Come conseguenza del seguente teorema abbiamo le seguenti proprietà

1. Due numeri interi consecutivi sono coprimi
2. Siano $a,b,c\in Z$ tali che $c|a\ast b$ con $c$ ed $a$ coprimi allora $c|b$
   1. Abbiamo che $9|3\ast 6$ però notiamo che $9\nmid 3$ infatti $c$ ed $a$ non sono coprimi
3. Siano $a,b,c\in Z$ tali che $a|c$ e $b|c$ se $a$ e $b$ sono coprimi allora $a\ast b|c$
   1. Abbiamo che $4|12$ e $6|12$ ma $24\nmid 12$ infatti $a$ e $b$ non sono coprimi

---

Fattorizzazione degli interi

Ogni intero n > 1 si può esprimere come prodotto di numeri primi positivi ed in modo unico Dimostrazione: la dimostrazione di questo teorema deve essere fatta in 2 passi distinti

1. Prima dimostriamo che preso un qualunque n > 1 esiste una fattorizzazione di n;
   • Se per assurdo esistessero interi > 1 che non sono prodotto di numeri primi positivi potremmo costruire l’insieme $S=n:n\in N$ con n che è un numero non prodotto di numeri primi. Per l’assioma del buon ordinamento, dentro questo insieme abbiamo un minimo che chiameremo $s$, $s$ non è primo (perché senno sarebbe un prodotto di numeri primi positivi) quindi vuol dire che ha almeno un divisore non banale positivo chiamato $d$, avendo un divisore vuol dire che esiste un intero positivo che $c$ che moltiplicato per $d$ ci da $s$, $c$ e $d$ sono prodotti di primi positivi, e quindi anche $s$ lo è
2. successivamente dimostriamo che quella fattorizzazione è unica
   • Se $n=p_1\cdot p_2\cdots p_r=q_1\cdot q_2\cdots q_s$ ovvero $n$ è la somma dei primi $r$ o $s$ numeri interi ($p_i$ e $q_i$ sono gli i-esimi numeri primi ). La dimostrazione che va fatta è che $r$ = $s$, di seguito la dimostrazione per induzione.
     • Caso base: $r=1$ Se $n=p_1$ allora $n$ è primo, da $p_1=q_1\cdot q_2\cdots q_s$ otteniamo che $s=1$ e $q_1=p_1$
     • Caso induttivo: supponendo che sia vera questa tesi per r, dimostriamola per r+1, quindi: $n=p_1\cdot p_2\cdots p_{r+1}=q_1\cdot q_2\cdots q_s$ , dal caso base sappiamo che $q_1$ è divisore di $p_1$ e che quindi dividendo membro a membro per $p_1$ otteniamo $p_2\cdots p_r\cdot p_{r+1}=q_2\cdots q_s$ da questo capiamo che $r=s-1$ e quindi che $s=r+1$ quindi i fattori coincidono a meno dell’ordine e quindi che sono uguali.

---

Teorema di Euclide

Il teorema di Euclide ci dice che i numeri primi sono infiniti. Dimostrazione:

1. Ipotesi per assurdo: Supponiamo che ci sia un numero finito di numeri primi. Se così fosse, potremmo elencarli tutti. Chiamiamo questi numeri primi $p_1,p_2,\dots ,p_n$, dove $p_1=2$, $p_2=3$, e così via fino a $p_n$, che rappresenterebbe l’ultimo numero primo.
2. Costruzione di un nuovo numero: Consideriamo il numero $h$ definito come il prodotto di tutti questi numeri primi più uno: $h=p_1\cdot p_2\cdots p_n+1$
3. Proprietà di $h$:
   • Per costruzione, $h$ è maggiore di tutti i numeri primi $p_1,p_2,\dots ,p_n$.
   • Inoltre, $h$ non è divisibile da nessuno dei numeri primi $p_1,p_2,\dots ,p_n$. Infatti, se dividiamo $h$ per uno qualsiasi di questi numeri primi $p_i$, otteniamo un resto di 1. In altre parole, $h\mathrm{mod}{p}_i=1$, per ogni $i=1,2,\dots ,n$.
4. Contraddizione:
   • A questo punto, possiamo concludere che $h$ o è primo oppure è divisibile da un numero primo non presente nella lista $p_1,p_2,\dots ,p_n$.
   • Se $h$ è primo, allora abbiamo trovato un nuovo numero primo che non era incluso nella lista originale, il che contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ fossero tutti i numeri primi.
   • Se $h$ non è primo, allora deve avere un divisore primo che non è nessuno dei $p_1,p_2,\dots ,p_n$, il che ancora una volta contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ siano tutti i numeri primi.

I numeri primi non solo sono infiniti, ma sono anche distribuiti in maniera tale da essere molto frequenti Sia $n\in N$ sia $\pi (n)$ il numero di numeri primi minori o uguali ad n. Allora ${\lim }_{n\to \infty }\frac{\pi (n)}{\frac{n}{\ln n}}=1$ da questo estraiamo la seguente formula: $\frac{n}{\ln n}$ che ci va ad indicare il numero di numeri primi < di n

• per $n=100$ stimati $\frac{100}{\ln 100}\approx 22$
• per $n=1000$ stimati $\frac{1000}{\ln 1000}\approx 145$

---

Come verificare se un numero n è primo?

Verificando che non abbia divisore diversi da quelli banali. Ciò può essere fatto in maniera più efficiente se durante la verifica consideriamo i numeri compresi tra 2 e $\sqrt{n}$

---

Crivello di Eratostene

Se abbiamo la necessità di calcolare tutti i numeri primi minori o uguali ad un numero n, possiamo usare il crivello di Eratostene, questi sono i passaggi da seguire:

1. Scriviamo in sequenza tutti i numeri naturali compresi tra 2 e n.
2. Partiamo dal numero 2 e cancelliamo tutti i suoi multipli
3. Ad ogni passo prendiamo il primo numero tra i numeri che seguono e cancelliamo i suoi multipli
4. Quando abbiamo cancellato tutti i multipli del numero più grande che sia minore o uguale $a\sqrt{n}$ ci fermiamo. Esempio

---

Radice numerica

Dato un numero $n$ la sua radice numerica di $n$, la denotiamo con $\rho (n)$ ed è la somma delle sue cifre reiterata sono ad ottenere una sola cifra

Esempio

$198:1+9+8=18\to 1+8=9$ e quindi $\rho (198)=9$.

---

Criteri di divisibilità

Esistono delle regole molto semplici per verificare la divisibilità di un numero $a$ per un numero $b$

• Divisibilità per 2: un numero è divisibile per $2$ se è pari
• Divisibilità per 3: un numero è divisibile per $3$ se la somma delle sue cifre è un numero divisibile per $3$
• Divisibilità per 5: un numero è divisibile per $5$ se l’ultima cifra è $0$ o $5$
• Divisibilità per 7: un numero è divisibile per $7$ se $q-2r$ è divisibile per $7$
• Divisibilità per 11: un numero è divisibile per $11$ se $a-b$ è divisibile per 11
• Divisibilità per 9: un numero $n$ è divisibile per $9$ se la sua radice numerica è divisibile per 9, oppure se $n-\rho (n)$ è divisibile per 9.
• Divisibilità per altri numeri primi:
  • $13$ divide n se $q+4r$ è divisibile per $13$
  • $17$ divide n se $q-5r$ è divisibile per $17$
  • $19$ divide n se $q+2r$ è divisibile per $19$
  • $23$ divide n se $q+7r$ è divisibile per $23$
    • $q=$ quoziente della divisione con $10$
    • $r=$ resto della divisione con $10$

Esempio

• Divisibilità per 7:
  • $q=$ quoziente della divisione con 10
  • $r=$ resto della divisione con 10
  • $161:16-2\ast 1=14$ che è divisibile per 7
• Divisibilità per 11:
  • $a=$ somma dei numeri nelle posizioni dispari
  • $b=$ somma dei numeri nelle posizioni pari
  • 2805 quindi con
    • $a=2+0$
    • $b=8+5$
    • $a-b=-11$ che è divisibile per 11
• Divisibilità per 9:
  • $198:1+9+8=18\to 1+8=9$ e quindi 198 è divisibile per 9
• Divisibilità per altri numeri: Esempi qui

---

Teorema della divisibilità per 9 Sia $n$ un numero naturale e sia $m$ la somma delle sue cifre. Allora $n-m$ è divisibile per 9. Dimostrazione: Sia $n$ un numero, rappresentato come:

• $n={\sum }_{i=0}^k{a}_i\cdot 10^i$ dove $a_0,a_1,\dots ,a_k$ sono le cifre del numero $n$, con $a_0$ che rappresenta le unità, $a_1$ le decine, e così via. Ora consideriamo un altro numero $m$, che ha la forma:
• $m={\sum }_{i=0}^k{a}_i$ Questo numero $m$ è la somma delle cifre di $n$. La differenza tra $n$ e $m$ è: $n-m={\sum }_{i=0}^k{a}_i\cdot 10^i-{\sum }_{i=0}^k{a}_i={\sum }_{i=0}^k{a}_i\cdot (10^i-1)={\sum }_{i=0}^k{a}_i\cdot 9\cdot b_i=9\cdot {\sum }_{i=0}^k{a}_i\cdot b_i$

Esempi

1. Consideriamo $n=199$. La somma delle cifre di $n$ è $m=1+9+9=19$. La differenza è: $199-19=180$ che è divisibile per 9.
2. Consideriamo $n=640$. La somma delle cifre di $n$ è $m=6+4+0=10$. La differenza è: $640-10=630$ che è divisibile per 9.
3. Consideriamo $n=1129$. La somma delle cifre di $n$ è $m=1+1+2+9=13$. La differenza è: $1129-13=1116$ che è divisibile per 9.

---

Dimostrazione per assurdo che $\sqrt{2}$ non è razionale

Assumendo che esistano 2 numeri naturali $a$ e $b$ tale che $\sqrt{2}=\frac{a}{b}$, assumendo anche che sia ridotta ai minimi termini almeno uno dei 2 è dispari. Elevando al quadrato otteniamo $a^2=2b^2$ essendo $a^2$ il doppio di un altro numero sarà per forza pari, detto ciò anche $a$ è pari è quindi esiste un numero $k$ tale che $a=2k$ da questo avremo allora:

• $2b^2=a^2=4k^2$ e quindi che anche $b$ è pari visto che $b^2=2k^2$ questa affermazione contraddice la nostra ipotesi inziale

---

Aritmetica modulare

L’aritmetica modulare riguarda il calcolo sui resti delle divisioni tra interi rispetto ad un divisore fissato. Ricordiamo la Divisione tra interi e diciamo che con la dicitura $n\mathrm{mod}m$, indichiamo con $n$ la base e con $m$ il modulo. Fissando un intero relativo $m$, possiamo definire la congruenza modulo $m$ in questo modo:

• un intero $a\in Z$ è in relazione con $b\in Z$ se $m|(a-b)$ e quindi che $a-b$ è un multiplo di $m$. In modo equivalente potemmo dire che $a$ è in relazione con $b$ se $a$ mod $b$ = $b$ mod $m$
• Se si verificano queste condizioni, la relazione tra a e b si scrive così:
  • $a\equiv b(\mathrm{mod}m)$
• Se non si verificano queste condizioni, la relazione tra a e b si scrive così:
  • $a\not\equiv b(\mathrm{mod}m)$

Formula generale per la congruenza

Diciamo che 2 numeri sono congruenti se è vero che $m|(a-b)$

Esempio

• 12 ≡ 9(mod 3) : $12$ mod $3$ = $9$ mod $3$ = $0$ entrambi per il primo caso del teorema della divisione
• $7\not\equiv 1(\mathrm{mod}4)$ infatti $7$ mod $4$ = $3$ mentre $1$ mod $4$ = $1$

TIP

Da tutto ciò notiamo che per ogni $a\in Z$ ed ogni $m\in N$ abbiamo che: $a\equiv a\mathrm{mod}m(\mathrm{mod}m)$ Esempio: $5\equiv 5\mathrm{mod}10(\mathrm{mod}10)$ se risolvi $5\mathrm{mod}10$ si capisce in modo intuitivo la proprietà

La relazione di congruenza è una relazione di equivalenza, il che implica che esistono un’infinità di classi di equivalenza, di seguito la dimostrazione:

• Riflessiva: Per ogni $a\in \mathbb{Z}$, è vero che $a\equiv a(\mathrm{mod}m)$. Infatti, la differenza $a-a=0$ è sempre divisibile per qualsiasi numero, incluso $m$, poiché $0$ è divisibile per ogni intero. Quindi, $a\equiv a(\mathrm{mod}m)$ per ogni $a\in \mathbb{Z}$.
• Simmetrica: Se $a\equiv b(\mathrm{mod}m)$ allora $a-b=km$ per qualche $k\in Z$ e quindi, moltiplicando per $-1$ otteniamo $-a+b=(-k)m$ ossia $b\equiv a(\mathrm{mod}m)$
• Transitiva: Se $a\equiv b(\mathrm{mod}m)$ e b ≡ $c(\mathrm{mod}m)$ abbiamo che esistono $h,k\in Z$ tali che $a-b$ = $hm$ e $b-c=km$. Sommando membro a membro le ultime due uguaglianze otteniamo: $a-c=(h+k)m$ e quindi $a\equiv c(\mathrm{mod}m)$.

---

Classi di equivalenza definite dalla congruenza

• Congruenza modulo 0: $a\equiv b(\mathrm{mod}0)$ se e solo se $a-b=k\cdot 0$ ovvero $a-b=0$ quindi se $a=b$
  • Tutte le classi di equivalenza create dalla congruenza modulo 0 sono delle classi contenenti un solo elemento (ovvero quello preso in esame)
    • In questo caso la classe di equivalenza di $a$ è {$a$}
• Congruenza modulo 1: $a\equiv b(\mathrm{mod}1)$ se e solo se $a-b=k\cdot 1$ ovvero $a-b$ è multiplo di 1
  • Essendo che ogni numero è multiplo di 1 la classe di equivalenza creata dalla congruenza modulo 1 contiene tutti gli interi $\in Z$
• Congruenza modulo 2: $a\equiv b(\mathrm{mod}2)$ se e solo se $a-b=k\cdot 2$ ovvero $a-b$ è un numero pari
  • Se $a$ è pari abbiamo che $a=2\ast h$ e quindi che $b=2h-k\ast 2=2(h-k)$ e quindi anche $b$ è pari
  • Se $a$ è dispari abbiamo che $a=2\ast h+1$ e quindi che $b=2h+1-k\ast 2=2(h-k)+1$ e quindi anche $b$ è dispari
  • Le classi di equivalenza create sono 2 una con tutti i numeri dispari e una con tutti i numeri pari Dato un intero m >= 0 indicheremo con $[a{]}_m$ la classe di rappresentata dall’intero $a$ nella relazione di congruenza modulo $m$ ovvero:
• $[a{]}_m=\{b\in \mathbb{Z}:a\equiv b(\mathrm{mod}m)\}$

Teorema Fissato un intero m > 1 le sue classi di equivalenza sono: $[0{]}_m,[1{]}_m,[2{]}_m,\dots ,[m-1{]}_m.$ Dimostrazione Sia $a\in Z$ e sia $r$ il resto della divisione intera di $a$ per $m$, ovvero, applicando l’algoritmo di divisione

• $a=qm+r$ con $0\le r<m$. Dal momento che $a-r=qm$ abbiamo che $a\equiv r(\mathrm{mod}m)$. Quindi, dal momento che $r$ può assumere solo i valori che vanno da $0$ a $m-1$ le classi di equivalenza sono solo quelle dell’enunciato del teorema.

Dimostrazione che le classi sono distinte Ragioniamo per assurdo e supponiamo che esistano $x,y\in Z$, $x\ne y$ e $0\le x$, $y<m-1$ tali che $[x{]}_m$ = $[y{]}_m$ . Senza perdita di generalità supponiamo che $x>y$. Dall’ipotesi possiamo scrivere $x-y=km$ cioè $x-y$ è un multiplo di $m$. Da $0\le x,y<m-1$ e $x>y$ segue che $0<x-y<m-1$, che è una contraddizione visto che non esistono multipli di $m$ in tra $0$ e $m-1$.

Sia $m=5$ (congruenza modulo $5$). Le classi resto modulo $5$ sono $[0{]}_5,[1{]}_5,[2{]}_5,[3{]}_5,[4{]}_5.$

Info

• $[2{]}_5$ Sono tutti quei numeri che divisi per 5 ci danno resto 2
• $[5{]}_{1}0$ Sono tutti quei numeri che divisi per 10 ci danno resto 5

Esercizio

Dato a ∈ Z come facciamo a stabilire in quale classe resto sta?

• La risposta ci viene fornita dal teorema appena dimostrato: $[a{]}_m$ = $[r{]}_m$ dove r è il resto della divisione di a per m.
• Quindi se m = 5 e a = 22 allora eseguendo la divisione abbiamo 22 : 5 = 4 con resto di 2, ottenendo che $[22{]}_5$ = $[2{]}_5$.
• Ricordiamo che la notazione $[a{]}_m$ indica la classe di equivalenza modulo $n$, cioè l’insieme di tutti i numeri interi che, divisi per $n$, lasciano lo stesso resto di $a$. Nel nostro caso:
  • $[22{]}_5$: Questa classe contiene tutti i numeri che, divisi per 5, lasciano resto 2. Alcuni esempi sono: 2, 7, 12, 17, 22, …
  • $[2{]}_5$​: Questa classe contiene tutti i numeri che, divisi per 5, lasciano resto 2. Alcuni esempi sono: 2, 7, 12, 17, …
  • le due classi contengono esattamente gli stessi elementi
• In altre parole potremmo dire che $22\equiv 2(\mathrm{mod}5)$

Notiamo che in classe $[0{]}_5$ ci sono tutti i multipli di 5 ed in generale in $[0{]}_m$ ci sono tutti i multipli di m.

---

Invarianza rispetto a somma e prodotto

Dato $m\in N$ e dati $a,b\in Z$ tali che $a\equiv b(\mathrm{mod}m)$ allora prendendo $c,d\in Z$ tali che $c\equiv d(\mathrm{mod}m)$ abbiamo che:

• $a+c\equiv b+d(\mathrm{mod}m)$
• $a\ast c\equiv b\ast d(\mathrm{mod}m)$

Dimostrazione:

Ipotizziamo che per ipotesi esistono $k_1$,$k_2$ tale che $a-b=k_{1}m$ e $c-d=k_{2}m$, da questo possiamo dimostrare che:

1. $(a+c)-(b+d)=(a-b)+(c-d)=(k_1$ + $k_2$)m (da questo capiamo che qualsiasi sia l’ordine delle lettere avremo sempre dei multipli di m)
2. Abbiamo $a=b+k_{1}m$ e $c=d+k_{2}m$ quindi $ac-bd=(b+k_{1}m)(d+k_{2}m)-bd=b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2=(b{k}_2+d{k}_1+k_1{k}_{2}m)m$

• Come si arriva a questa conclusione? 1. Sfruttiamo le ipotesi: Ricordiamo che per ipotesi abbiamo: - $a\equiv b(\mathrm{mod}m),$ quindi $a=b+k_{1}m$ - $c\equiv d(\mathrm{mod}m),$ quindi $c=d+k_{2}m$ 2. Sostituiamo nella moltiplicazione: Moltiplichiamo membro a membro le due equazioni ottenute al punto precedente: - $ac=(b+k_{1}m)(d+k_{2}m)$ 3. Sviluppiamo il prodotto: Svolgendo i calcoli otteniamo: - $ac=bd+b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2$ - $ac-bd=b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2$ 4. Evidenziamo m: Mettiamo in evidenza m a secondo membro: - $ac-bd=m(b{k}_2+d{k}_1+k_1{k}_{2}m)$ 5. Cosa significa questo risultato? - Abbiamo dimostrato che la differenza tra $ac$ e $bd$ è un multiplo di $m$. Quindi, per definizione di congruenza modulo $m$, si ha: $ac\equiv bd(\mathrm{mod}m)$

---

Casi particolari:

• Invarianza rispetto alla somma 1: Se sommiamo ad entrambi i membri di una congruenza uno stesso numero intero, la congruenza non cambia
  • $a\equiv b(\mathrm{mod}m)$ allora $a+c\equiv b+c(\mathrm{mod}m)$
• Invarianza rispetto al prodotto 1: Se moltiplichiamo ambo i membri di una congruenza per uno stesso numero intero, la congruenza non cambia.
  • $a\equiv b(\mathrm{mod}m)$ allora $ac\equiv bc(\mathrm{mod}m)$
• Invarianza rispetto alla somma 2: Se sottraiamo ad entrambi i membri di una congruenza uno stesso numero intero, la congruenza non cambia
  • $a\equiv b(\mathrm{mod}m)$ allora $a-c\equiv b-c(\mathrm{mod}m)$
• Invarianza rispetto al prodotto 2: Se dividiamo ambo i membri di una congruenza per uno stesso numero intero, la congruenza potrebbe non valere più.
  • $6\equiv 0(\mathrm{mod}3)$ è vera se dividiamo tutto per 2 diventa $2\not\equiv 0(\mathrm{mod}3)$ che è falsa

---

Conseguenza dei casi particolari:

Come conseguenza dei primi 2 casi particolari, dati $a,b,m\in N$ e visto che $a\equiv a\mathrm{mod}m(\mathrm{mod}m)$ e $b\equiv b\mathrm{mod}m(\mathrm{mod}m)$ valgono le seguenti proprietà:

1. $(a+b)$ ≡ $(a\mathrm{mod}m+b\mathrm{mod}m)(\mathrm{mod}m)$ ossia $(a+b)\mathrm{mod}m$ = $(a\mathrm{mod}m+b\mathrm{mod}m)(\mathrm{mod}m$)
2. $(a\times b)$ ≡ $(a\mathrm{mod}m\times b\mathrm{mod}m)(\mathrm{mod}m)$ ossia $(a\times b)\mathrm{mod}m=((a\mathrm{mod}m)(b\mathrm{mod}m))(\mathrm{mod}m)$ Come conseguenze del punto 2 abbiamo:
3. Dati $a,n,m\in N,a^2\equiv (a\mathrm{mod}m{)}^2(\mathrm{mod}m)$
4. Dati $a,b,h,k,m\in N$ allora $a^h\times b^k\equiv (a^h\mathrm{mod}m)\times (b^k\mathrm{mod}m)(\mathrm{mod}m)$ ossia $a^h\times b^k\mathrm{mod}m=(a\mathrm{mod}m{)}^h\times (b\mathrm{mod}m{)}^k\mathrm{mod}m$

---

Diretta conseguenza dell’invarianza rispetto alla somma

Teorema:

• Per ogni $m\in N,m>1$ , prendendo una qualunque sequenza di m interi questa contiene un intero divisibile per m Dimostrazione: Consideriamo allora $m$ interi consecutivi, dove il più piccolo è $n$, Come abbiamo già dimostrato, le classi di equivalenza della relazione di congruenza modulo $m$ sono $[0{]}_m,[1{]}_m,[2{]}_m,...[m-1{]}_m$ , il nostro numero $n$ si trova in una di queste classi di equivalenza, supponiamo stia nella classe $[i{]}_m$ per $0\le i\le m-1$. Quindi $n\equiv i(\mathrm{mod}m)$ ed allora $n+1\equiv i+1(\mathrm{mod}m)$ ovvero $n+1\in [i+1]m$. Notiamo allora che se $i=0$ ovvero $n\in [0{]}_m$ abbiamo dimostrato il teorema. Se invece $i>0$, visto che $0<i<m$ incrementando $i$ esattamente $m-i$ volte, con $m-i<m$ otteniamo che $n+(m-i)\equiv i+(m-i)(\mathrm{mod}m)$ ossia $n+(m-i)\equiv m(\mathrm{mod}m)\equiv 0(\mathrm{mod}m)$. In conclusione, $n+(m-i)$ è il numero multiplo di $m$ nella sequenza di $m$ numeri consecutivi.

---

Esercizi:

---

Inverso modulare

Nei numeri razionali esiste il concetto di “inverso” ovvero preso $a\in Q$ e $a\ne$ 0 esiste un $x\in Q$ tale che $a\ast x=1$, $x$ viene anche denotato con la dicitura $a^{-1}$.

• se $a=2$ allora $a^{-1}=\frac{1}{2}$ Il seguente teorema introduce una nozione simile per l’aritmetica modulare.

Teorema Siano $a,b\in N$ entrambi maggiori di zero. Allora, esiste un elemento $x\in N$ tale che $a\cdot x\equiv 1(\mathrm{mod}b)$ se e solo se $a$ e $b$ sono coprimi. Anche in questo caso l’elemento x viene detto “inverso di a modulo b” e si denota con $a^{-1}$

Esempi

• con $a=5$, $b=3$ abbiamo che $a^{-1}$ = $2$,
  • infatti $2\cdot 5$ mod $3$ = $10$ mod $3$ = $1$ che è congruo con $1$ mod $3$
• con $a=9$, $b=7$ abbiamo che $a^{-1}$ = $4$,
• infatti $4\cdot 9$ mod $7$ = $36$ mod $7$ = $1$ che è congruo con $1$ mod $7$

Dimostrazione

---

Funzione di Eulero

Sia $n$ un intero positivo per definire quanti sono i numeri che precedono $n$ e che sono anche coprimi con $n$ dobbiamo usare la funzione di Eulero definita così:

• $\varphi (n)=|\{x:x\in \mathbb{N},0<x\le n,MCD(n,x)=1\}|$ La funzione phi di Eulero di n è uguale al numero di numeri naturali x, compresi tra 0 e n (estremi inclusi), tali che il massimo comune divisore tra n e x sia uguale a 1.

Esempi

$n=5$ : φ(5) = 4 poiché MCD(5, x) = 1, per x = 1, 2, 3, 4. $n=7$: φ(7) = 6 poiché MCD(7, x) = 1, per x = 1, 2, 3, 4, 5, 6. $n=10$: φ(10) = 4 poiché MCD(10, x) = 1, per x = 1, 3, 7, 9. $n=12$: φ(12) = 4 poiché MCD(12, x) = 1, per x = 1, 5, 7, 11.

---

Formule generali per il calcolo del $\varphi (n)$ usata negli esercizi

Ci sono delle formule generali per il calcolo del phi di un numero:

1. Se $n$ è un numero primo tutti i predecessori di n sono ad esso coprimi quindi $\varphi (n)=n-1$
2. Il caso $n$ potenza di numero primo, ovvero $n=p^k$ dove $k\ge 2$ e $p$ è primo, tutti i divisori di $n$ vanno da $p^1,p^2,\dots ,p^k$ e i multipli di $p$ sono $p,2p,3p,\dots ,p^{k-1}$ i multipli di $p$ sono i numeri non coprimi con $n$, quindi facendo la differenza tra $p^k$ e $p^{k-1}$ otteniamo tutti i numeri coprimi con n ovvero $\phi (n)=\phi (p^k)=n-p^{k-1}=p^k-p^{k-1}$
3. Analizziamo il caso $n$ prodotto di due numeri distinti, ovvero n = $p_1\ast p_2$ con $p_1,p_2$ entrambi primi. Tra gli interi $1,2,3,...p_1\cdot p_2$ = $n$ ci sono $p_2$ multipli di $p_1$, ossia $p_1$, $2p_1$, $3p_1$, … , $p_2$ · $p_1$ e, analogamente $p_1$ multipli di $p_2$. Tolti i multipli di $p_1$ e di $p_2$ tutti gli altri interi sono ovviamente coprimi con $n$ e quindi φ(n) = n − $p_1$ − $p_2$ + 1 = $p_1{p}_2$ − $p_1$ − $p_2$ + 1 = ($p_1$ − 1) · ($p_2$ − 1)

Esempi

$\phi (5)=4$ $\phi (8)=\phi (2^3)=2^3-2^2=8-4=4$ $\phi (6)=\phi (2\cdot 3)=(2-1)\cdot (3-1)=2$

Il caso numero 3 può essere generalizzato nel seguente modo: Sia $n=h\cdot k$ dove $h$ e $k$ sono interi maggiori di zero e coprimi tra di loro. Allora $\phi (n)=\phi (h)\cdot \phi (k)$

• φ(4 · 9) = φ($2^2$) · φ($3^2$) = 2 · 6 = 12
• φ(5 · 8) = φ($5$) · φ($2^3$) = 4 · 4 = 16

Formulario

• Per n numero primo allora $\phi (n)=n-1$
• Con n multiplo di un numero primo φ(n) = $n^{k_1}$ - $n^{k_2-1}$
• Con n prodotto di numeri primi $\phi (n)=\phi (k)\times \phi (q)...$

---

Formula generale per il calcolo della funzione di Eulero

Utilizzando il teorema di fattorizzazione degli interi possiamo ricavare la formula generale per il calcolo della funzione φ di Eulero. Sia n > 1, consideriamo la sua fattorizzazione $n=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_m^{k_m}$ Allora

• $\varphi (n)=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_m^{k_m}-p_m^{k_m-1})$

Dimostrazione: dimostriamo il teorema per induzione sul numero dei fattori primi presenti nella fattorizzazione di n. Caso base: se $m=1$ allora $p_1^{k_1}$ sappiamo che è vera per il caso 2 Passo induttivo: Supponiamo il teorema sia vero per ogni intero $n^{\prime }$ la cui fattorizzazione presenta $m-1$ primi diversi campiamo che $n^{\prime }=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_{m-1}^{k_{m-1}}$ a questo punto la fattorizzazione per $m$ sarà uguale a:

• $n=n\prime \cdot p_m^{k_m}$ dal teorema abbiamo che: $\varphi (n^{\prime })=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_{m-1}^{k_{m-1}}-p_{m-1}^{k_{m-1}-1})$ e quindi $\varphi (n)=\varphi (n^{\prime })\ast (p_m^{k_m}-p_m^{k_m-1})$.

Come possiamo notare il teorema vale sia nel caso base, sia nel passo induttivo e quindi il teorema è dimostrato.

Esempio

$\phi (42)=(2^1-2^{1-1})\cdot (3^1-3^{1-1})\cdot (7^1-7^{1-1})=$ $=(2^1-2^0)\cdot (3^1-3^0)\cdot (7^1-7^0)$ Quindi $\phi (42)=1\cdot 2\cdot 6=12$. In questo esempio ho preferito specificare ogni singolo esponente per renderlo più semplice da capire)

---

Teorema di Eulero

Il seguente teorema, detto Teorema di Eulero, dimostra come la funzione φ di Eulero si possa applicare alla esponenziazione modulare. Siano $n,m$ > $0$, se $MCD(n,m)=1$ allora $n^{\phi (m)}\equiv 1(\mathrm{mod}m)$

Esempio

$n=12,m=5:12^4\equiv 1(\mathrm{mod}5)$ infatti $12^4=20736$ e $20736\mathrm{mod}5=1$

Dimostrazione da non studiare per l’esame

---

Piccolo teorema di Fermat

conosciuto come “Ultimo Teorema di Fermat” afferma che non esistono soluzione intere positive all’equazione $a^n+b^n=c^n$ per $n>2$

Teorema Se $p$ è primo e $MCD(a,p)=1$, ovvero a non è un multiplo di $p$, allora $a^{p-1}\equiv 1(\mathrm{mod}p)$

Esempio

---

Altra conseguenza del teorema di Eulero

Se $MCD(a,n)=1$, allora per ogni $x>0$ vale la seguente cosa:

• $a^x\equiv a^{x\mathrm{mod}\phi (n)}(\mathrm{mod}n)$

---

Calcolo dell’inverso modulare

Abbiamo visto che se n ed m sono comprimi, allora esiste l’inverso di n modulo m ossia esiste k tale che $n\ast k\equiv 1(\mathrm{mod}m)$, per calcolare l’inverso di $n$ modulo $m$ è:

• $(n\mathrm{mod}m{)}^{\phi (m)-1}\mathrm{mod}m$

Esempio

Esercizi qui

---

Applicazioni dell'aritmetica modulare

La prova del 9

La prova del nove è una verifica di correttezza del risultato di una operazione aritmetica tra numeri interi, ricordando la definizione di radice numerica questo è il teorema che definisce la prova del 9: Teorema: dati $n,m\in N$ abbiamo che:

• $\rho (n\ast m)=\rho (\rho (n)\ast p(m))$
• $\rho (n+m)=\rho (\rho (n)+p(m))$

Esempio

Verificare che $123\ast 347$ Faccia $42671?$ per verificare che è giusto facciamo così:

• $\rho (123)=6$
• $\rho (347)=5$
• $\rho (\rho (123)\ast \rho (347))=\rho (30)=3$
• $\rho (42671)=\rho (20)=2$

Gli ultimi 2 risultati sono sbagliati quindi la moltiplicazione è stata fatta nel modo errato (il vero risultato di $123\ast 347$ è $42681$)

Teorema: dato $n\in N$ abbiamo che $n\equiv \rho (n)(\mathrm{mod}9)$ in pratica stiamo dicendo che la radice numerica di un qualsiasi numero è congrua modulo $9$.

Dimostrazione: per il Teorema di divisibilità del $9$ sappiamo che dato $n\in N$, se $m$ è la somma delle sue cifre allora $n-m$ è divisibile per $9$, ossia esiste un $k$ tale che $n-m=9k$. Quindi, ottengo che $n\equiv m(\mathrm{mod}9)$. Reiterando, se $m\prime$ è la somma delle cifre di $m$ otteniamo $m\equiv m\prime (\mathrm{mod}9)$ quindi $n\equiv m(\mathrm{mod}9)\equiv m\prime (\mathrm{mod}9)$. Fermiamo il processo di somma delle cifre quando otteniamo un numero con una sola cifra (ovvero la radice numeri di $n$) quindi concludiamo che $n\equiv \rho (n)(\mathrm{mod}9)$

Esempio

• $250\equiv 7\mathrm{mod}9$ infatti
  • $250\mathrm{mod}9=7$
  • $7\mathrm{mod}9=7$

---

Codice ISBN

Il codice ISBN è un codice identificativo standard per i libri , oggi è composto da 13 cifre mentre prima del 2007 era composto da 10 cifre. Per controllare la validità del codice si fa in questo modo:

• ISBN-10: Se le cifre sono da $a_{10}$ fino ad $a_1$ il codice è formalmente corretto se:
  • $a_1+2a_2+3a_3+\cdots +9a_9+10a_{10}\equiv 0(\mathrm{mod}11)$

Esempio

Il codice 2468864212 è corretto?

• Abbiamo $10\cdot 2+9\cdot 4+8\cdot 6+7\cdot 8+6\cdot 8+5\cdot 6+4\cdot 4+3\cdot 2+2\cdot 1+2=264$
• il numero è divisibile per 11 quindi è un codice ISBN-10 corretto.

• ISBN-13: se le cifre sono da $a_1$ fino ad $a_{13}$ il codice è formalmente corretto se:
  • $a_1+3a_2+a_3+3a_4+\cdots +a_9+3a_{10}+a_{11}+3a_{12}+a_{13}\equiv 0(\mathrm{mod}10)$

Esempio

• Il codice 2468864211129 è corretto?
• Abbiamo $2+12+6+24+8+18+4+6+1+3+1+6+9=100$
• il numero è divisibile per 10 quindi è un codice ISBN-13 corretto

---

Codice carta di credito

Anche il codice numerico a 16 cifre si basa sull’aritmetica modulare, assumendo che le cifre siano le seguenti (raggruppate in 4 gruppi):

• $a_1{b}_1{a}_2{b}_2$
• $a_3{b}_3{a}_3{b}_3$
• $a_5{b}_5{a}_6{b}_6$
• $a_7{b}_7{a}_8{b}_8$ Il codice numerico della carta di credito è formalmente corretto se $S$ è divisibile per 10 con $S={\sum }_{i=1}^8\rho (2a_i)+{\sum }_{i=1}^8{b}_i$

Esempio

• 1234-5678-8765-4321
  • Le cifre di posto dispari, quelle che abbiamo denotato con $a_i$ sono allora 1, 3, 5, 7, 8, 6, 4, 2 moltiplicando per 2 e sommando le cifre dei risultati a più di una cifra otteniamo i numeri: 2, 6, 1, 5, 7, 3, 8, 4 la cui somma è 36
  • Le cifre di posto pari, quelle che abbiamo denotato con $b_i$ sono allora 2, 4, 6, 8, 7, 5, 3, 1 e la somma da come risultato di nuovo 36.
• Quindi, non è un numero di carta di credito corretto, visto che il risultato finale 36 + 36 = 72 non è un multiplo di 10.

---

Cifrari a trasposizione

Teoria dei numeri e problemi aperti

Ci sono molti problemi della teoria dei numeri che sono ancora irrisolti di seguito i problemi aperti più famosi, la maggior parte dei problemi aperti saranno del tipo “questa sequenza numeri è infinità?“. Quasi tutte le sequenze più famose le trovi su questo sito: OEIS

Numeri primi di Mersenne

I numeri primi di Mersenne sono numeri primi della forma:

• $M_p=2^p-1$
  • $M_2=2^2-1=3$
  • $M_3=2^3-1=7$ Ad oggi conosciamo solo 52 numeri di Mersenne, l’ultimo scoperto ad ottobre 2024 grazie al progetto GIMPS lista numeri di Mersenne , il problema aperto è se questa sequenza sia infinita.

Numeri perfetti: funzione “Sigma”

Dato un numero $n\in N$ definiamo la seguente funzione

• $\sigma (n)={\sum }_{0<d,d|n}d$ ovvero la somma di tutti i divisori positivi di un numero. un numero si dice perfetto se $\sigma (n)=2n$ il primo numero perfetto è il 6 infatti:
• $\sigma (6)=1+2+3+6=12$ I primi a studiare questi numeri furono i pitagorici. Pitagora si accorse di una proprietà che fu poi dimostrata da Euclide, ossia che se $2^n-1$ è un numero primo allora $2^{n-1}\ast (2^n-1)$ è perfetto Infatti i numeri perfetti sono strettamente correlati ai numeri di Mersenne, cosi quest’ultimi si ci chiede se i numeri perfetti siano infiniti.

Numeri primi gemelli

I numeri primi gemelli sono coppie di numeri primi che hanno una differenza di $2$, come $(3,5),(5,7)$, ecc. Entrambi i numeri sono dispari, perché la loro differenza è $2$, un numero pari.

La domanda riguarda se esistono infinite coppie di numeri primi la cui differenza è pari a $2k$ per ogni $k\ge 1$. Questo è legato alla congettura delle coppie di numeri primi, che suggerisce che esistano infinite coppie di numeri primi con differenze fisse, ma non è ancora stata dimostrata. In altre parole, pur essendo noti molti esempi, la dimostrazione formale che esistano infiniti numeri primi gemelli o con differenze maggiori è ancora un mistero aperto.

Congettura di Goldbach

La congettura di Goldbach, proposta dal matematico prussiano nel 1742 e formulata da Eulero, afferma che ogni numero pari maggiore di 4 può essere scritto come la somma di due numeri primi. Ad esempio:

• $6=3+3$
• $8=3+5$
• $10=3+7=5+5$
• $12=5+7$
• $14=3+11=7+7$

La congettura non è ancora stata dimostrata, ma non è stato trovato nemmeno un numero pari che non soddisfi questa proprietà.

Esistono due definizioni equivalenti della congettura:

1. G1: Per ogni numero intero $x\ge 2$, esiste un intero $d\ge 0$ tale che $x-d$ e $x+d$ siano entrambi numeri primi.
2. G2: Per ogni numero intero $x\ge 2$, esistono due numeri primi $p_1$ e $p_2$ tali che $x=\frac{p_1+p_2}{2}$.

In altre parole, la congettura suggerisce che ogni numero pari può essere rappresentato come la media di due numeri primi.

Un concetto importante nella discussione della congettura di Goldbach è il concetto di separatori dei numeri primi gemelli, ovvero gli interi che si trovano a metà tra due numeri primi consecutivi. Per esempio, la sequenza di “interprimi” contiene numeri come $4$, $6$, $9$, $12$, $15$, $18$, $21$, ecc. Questi numeri, che si trovano a metà tra due numeri primi consecutivi, verificano la congettura di Goldbach. Ad esempio, $9$ è la media di $7$ e $11$, che sono numeri primi consecutivi.

Inoltre, grazie ai moderni strumenti di calcolo, la congettura è stata verificata fino a numeri pari molto grandi, fino a circa $10^{17}$, ma non è stata ancora dimostrata in modo generale.

Un’altra parte interessante della congettura riguarda la distanza di Goldbach, definita come la distanza minima $d(n)$ per ogni numero $n$, tale che $n-d(n)$ e $n+d(n)$ siano entrambi numeri primi. Per esempio:

• $d(2)=0$ (poiché $2$ è primo),
• $d(4)=1$ (poiché $3$ e $5$ sono primi),
• $d(6)=1$ (poiché $5$ e $7$ sono primi),
• $d(8)=3$ (poiché $5$ e $11$ sono primi).

Le sequenze di numeri con distanze di Goldbach uguali a un certo valore $k$ formano diverse classi di numeri, come la sequenza $G1$ (separatori dei primi gemelli), $G2$, $G3$, ecc. La congettura di Goldbach sarebbe vera se queste sequenze coprissero tutti i numeri naturali (eccetto $0$ e $1$).

Tuttavia, ci sono molte incognite, come la domanda se esistano sequenze infinite (ad esempio, se esistano infiniti separatori di primi gemelli) o sequenze vuote (se esistano valori di $d$ tali che non ci siano numeri $n$ per cui $n-d$ e $n+d$ sono entrambi primi).

In sintesi, la congettura di Goldbach suggerisce che ogni numero pari maggiore di $4$ è la somma di due numeri primi, ma non è ancora stata provata in modo rigoroso.

Congettura di Collatz

La congettura di Collatz conosciuta anche come congettura $3x+1$ questa congettura lega la teoria dei numeri ad un problema di terminazione di un algoritmo iterativo. L’algoritmo si basa sulla seguente funzione: 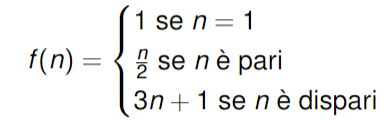Che diventa in pseudocodice:

Algoritmo di Collatz 
Leggi un intero x ≥ 1 
while (x > 1) do 
	if x mod 2 == 0 x = x/2; 
	else x = 3 ∗ x + 1; 
end_while

Il problema irrisolto: l’algoritmo si ferma sempre oppure esiste un $x$ partendo dal quale non si raggiunge mai il valore $1$?

L’algoritmo produce una sequenza di interi detta traiettoria di n dove n è il numero in input. Di seguito l’output di un’implementazione in C della seguente congettura con la traiettoria dei primi 10 numeri: 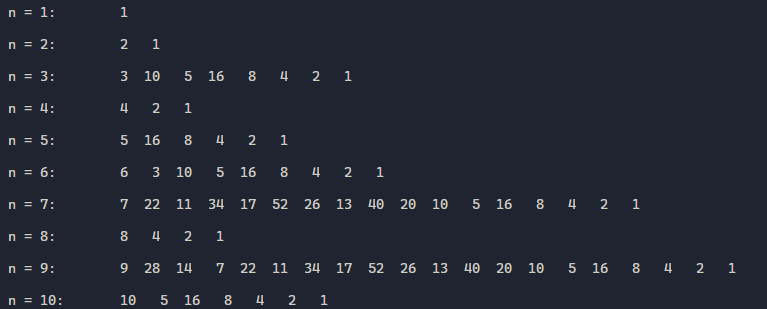Notiamo che per alcuni interi la lunghezza della traiettoria è maggiore del numero stesso ($n=3$ ad esempio). Con il tempo è stato ideato un algoritmo di collatz semplificato

Algoritmo di Collatz semplificato 
Leggi un intero x ≥ 1 
while (x > 1) do 
	if x mod 2 == 0 x = x/2; 
	else x = (3 ∗ x + 1)/2; 
end_while

Visto che x è dispari, sicuramente 3x + 1 è pari, e quindi possiamo direttamente assegnare come nuovo valore ad x il valore (3x + 1)/2. In questo modo le traiettorie di accorciano. Sebbene la congettura sia stata formulata nel 1937, gran parte del lavoro “sperimentale” per provare a risolverla è incominciato nel 1970. Ad oggi, la congettura è stata verificata per tutti gli $n<10^{18}$