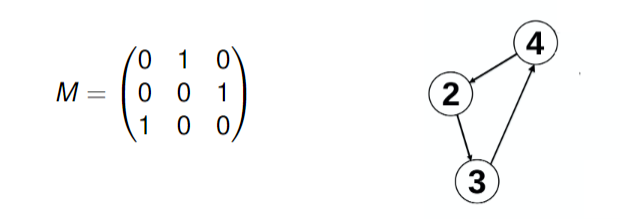Questo file è la rielaborazione delle slide 04_Parte4
Teoria dei grafi
La teoria dei grafi inizia per risolvere un problema reale, chiamato problema dei sette ponti, questi ponti sono situati in una città Russa attraversata da un fiume e presenta due isolette che sono collegate con le aree principali della città con 7 ponti. Il nostro caro Eulero era in città e venne a sapere di questo problema: “E’ possibile fare una passeggiata che
attraversi ogni ponte una sola volta?”
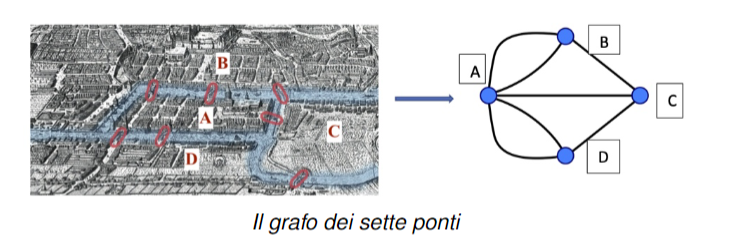 Eulero sintetizza il tutto in termini astratti, assegnando ad ogni area della città un nodo e ad ogni ponte un arco.
Eulero sintetizza il tutto in termini astratti, assegnando ad ogni area della città un nodo e ad ogni ponte un arco.
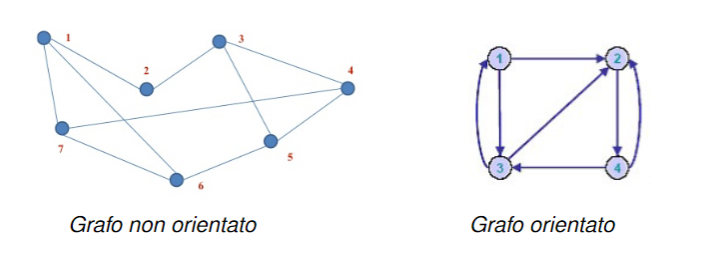
Definizione di grafo non orientato
Un grafo semplice non orientato denotato con è formato da:
- un insieme finito di nodi/vertici ()
- un insieme finito di archi () dove ogni elemento di è un sottoinsieme di cardinalità 2 di fatto in questo modo con
- Due nodi che caratterizzano l’arco sono detti “estremi dell’arco” e si dicono adiacenti
- Un arco che ha come estremo il nodo si dice “incidente” ad .
- Un vertice che non è l’estremo di alcun arco si dice “isolato”.
Definizione di grafo orientato
Un grafo semplice orientato denotato con consiste:
- un insieme finito di nodi/vertici
- un insieme finito di archi in questo caso però gli elementi che appartengono ad sono delle coppie ordinate. Di conseguenza gli archi avranno un verso. Gli archi del tipo ovvero degli archi orientati da un nodo verso se stesso vengono detti cappi.
Rappresentazione dei grafi
Rappresentiamo i grafi nel piano in questo modo
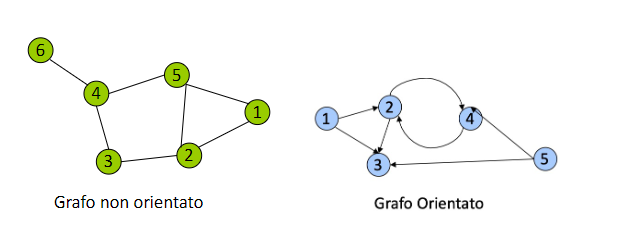 Come possiamo notare da questa rappresentazione gli archi dei grafi orientati hanno una direzione.
Come possiamo notare da questa rappresentazione gli archi dei grafi orientati hanno una direzione.
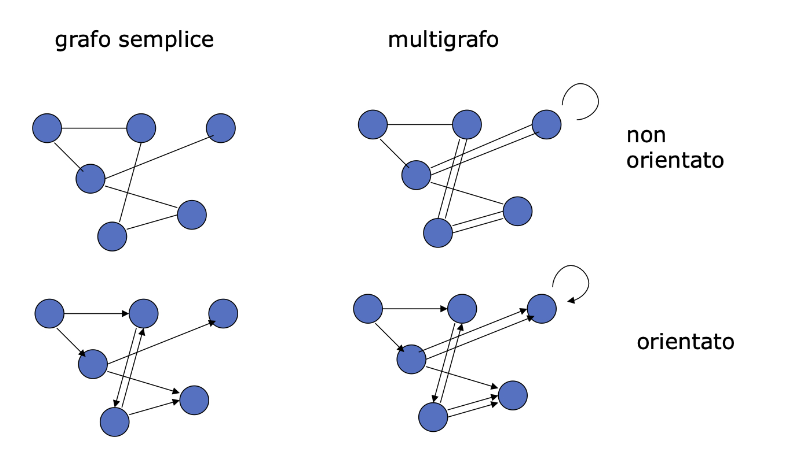
Multigrafi
I grafi dove troviamo più di un arco che collega coppie di nodi sono detti “multigrafi”.
Grado di un nodo
Dato un grafo il grado di un nodo denotato con è il numero di archi ad esso incidenti ovvero:
- il grado del vertice è uguale al numero di archi nell’insieme (insieme di tutti gli archi del grafo) tali che il vertice è uno degli estremi dell’arco
Dato un grafo orientato abbiamo 2 definizione differenti di grado di un nodo:
- Grado di ingresso : ovvero il numero di archi orientati che “entrano” in
- il grado di ingresso del nodo è pari alla cardinalità dell’insieme formato da tutti gli archi del tipo
- Grado di uscita : ovvero il numeri di archi orientati che “escono” da
- il grado di uscita del nodo è pari alla cardinalità dell’insieme formato da tutti gli archi del tipo
Esempio con grafo non orientato
Di seguito i gradi dei vari nodi di questo grafo non orientato:
- δ(1) + δ(2) + δ(3) + δ(4) + δ(5) + δ(6) = 2 + 3 + 2 + 3 + 3 + 1 = 14
Esempio con grafo orientato
Di seguito i gradi dei vari nodi di questo grafo non orientato:
Da questi esempi notiamo che:
- Grafo non orientato: la somma di tutti i gradi è il doppio del numero degli archi
- Grafo orientato: la somma dei gradi in ingresso è uguale alla somma dei gradi in uscita, e la somma totale è il doppio del numero degli archi del grafo.
Handshaking Theorem
Sia un grafo non orientato allora la somma dei gradi di ogni vertice è uguale al doppio del numero degli archi.
Grafi regolari
Dato un grafo non orientato si dice regolare se tutti i suoi nodi hanno lo stesso grado , la cardinalità di ovvero il numero di vertici del grafo è uguale a:
Esempio
Consideriamo un grafo regolare con 4 vertici e grado 2 (r = 2). Ciò significa che ogni vertice è connesso a esattamente altri due vertici. Un esempio potrebbe essere un quadrato, dove ogni vertice è connesso ai due vertici adiacenti. In questo caso ci sono 4 spigoli , quindi |E| = 4. Applicando la formula:
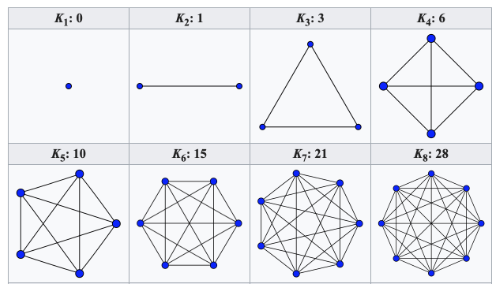
Grafi completi
Diciamo che è completo se ogni coppia di vertici è connessa da un arco. Se allora il numeri di archi del grafo completo è ovvero il numero di tutte le possibili coppie di vertici.
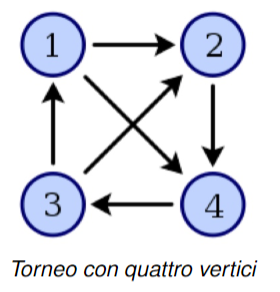
Torneo
Sia un grafo completo. Il grafo orientato ottenuto assegnando uno dei due possibili versi ad ogni arco di , si dice torneo, l’arco tra ogni coppia è orientato dal vincitore al perdente
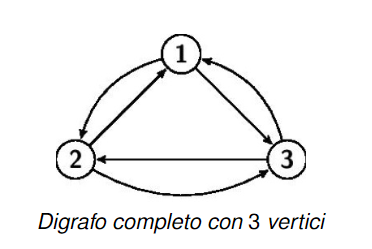
Grafi orientati completi
La definizione di grafo completo si estende anche ai grafi orientati, sia un grafo orientato diciamo che è completo se ogni coppia ordinata è connessa da un arco, ovvero per ogni coppia di vertici abbiamo e
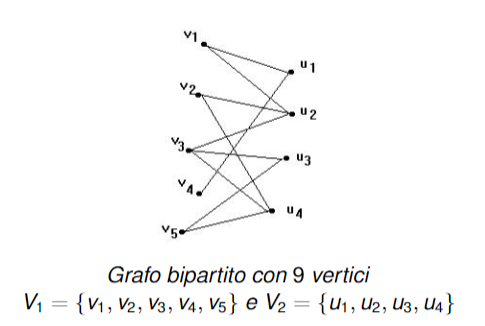
Grafi bipartiti
Sia un grafo non orientato. Diciamo che è bipartito se possiamo partizionare (l’insieme dei vertici) in 2 insiemi solitamente denotati con e in maniera tali che tutti gli archi abbiano un estremo in entrambi gli insiemi e
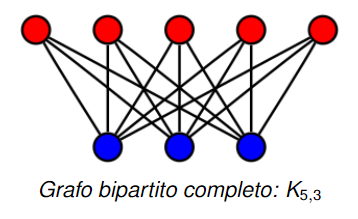
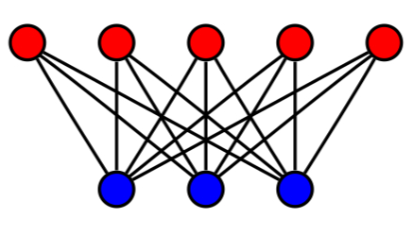
Grafi bipartiti completi
Il grafo bipartito si dice completo se definita la partizione dei vertici e esiste un arco per ogni coppia di vertici e . Un grafo bipartito completo si indica con dove e
Sottografo
Sia un grafo non orientato. Diciamo che è un sottografo di se:
- Ogni arco ha i suoi estremi entrambi in
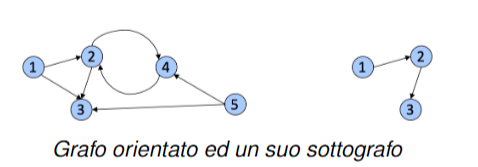
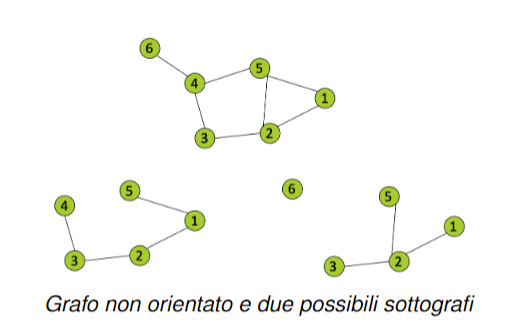 Questa stessa regola vale anche per i grafi orientati, ovviamente i sottografi che possiamo creare saranno anche essi orientati.
Questa stessa regola vale anche per i grafi orientati, ovviamente i sottografi che possiamo creare saranno anche essi orientati.
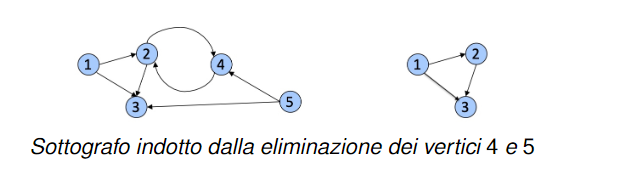
 Sottografo indotto
Sia , dato . Il sottografo indotto da è il sottografo ottenuto eliminando da tutti i vertici non appartenenti a e tutti gli archi incidenti ad almeno uno dei vertici eliminati
Sottografo indotto
Sia , dato . Il sottografo indotto da è il sottografo ottenuto eliminando da tutti i vertici non appartenenti a e tutti gli archi incidenti ad almeno uno dei vertici eliminati
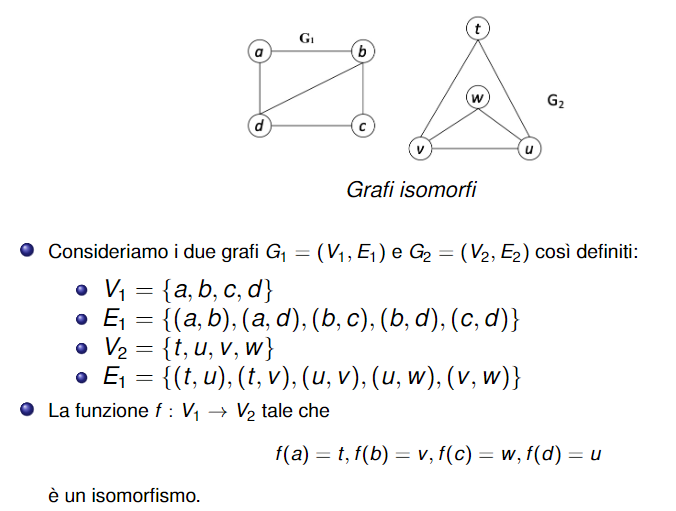
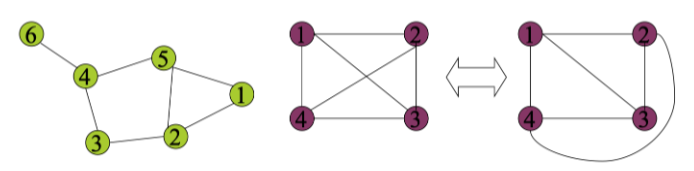
Grafi isomorfi
Di seguito cercheremo di rispondere alla domanda: “In che modo 2 grafi possono essere considerati uguali?”
Definizione di Isomorfismo tra grafi: Due grafi e si dicono isomorfi se esiste una applicazione biunivoca dall’insieme dei vertici all’insieme dei vertici tale che () è un arco di se e solo se è un arco di
Esempio
Come immediata conseguenza sappiamo che:
- e
- essendo allora nel caso di grafi non orientati, e e nel caso di grafi orientati
- dato un sottografo del primo grafo esiste un sottografo del secondo a cui è isomorfo
Esempio
Questi 2 grafi hanno lo stesso numero di vertici e archi, però notiamo subito che non sono isomorfi perché nel grafo il vertice 2 ha gradi uscita pari a 2 mentre nessun vertice in ha questo grado di uscita.
Omeomorfismi
Di seguito cercheremo di rispondere alla seguente domanda: “in che modo 2 grafi possono essere interpretati come aventi la stessa forma?”
Definizione di suddivisione di un arco non orientato
Sia un grafo non orientato e sia un arco di G. Una suddivisione dell’arco è ottenuta introducendo un nuovo vertice w e sostituendo in l’arco con gli archi e
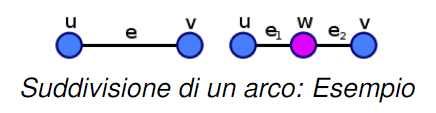
Definizione di suddivisione di un arco orientato
Sia un grafo orientato e sia un arco di G. Una suddivisione dell’arco è ottenuta introducendo un nuovo vertice w e sostituendo in l’arco orientato con gli archi orientati e

Omeomorfismo tra grafi
Due grafi non orientati e si dicono omeomorfi se attraverso una serie di suddivisioni di archi e si possono ottenere due grafi e che sono isomorfi
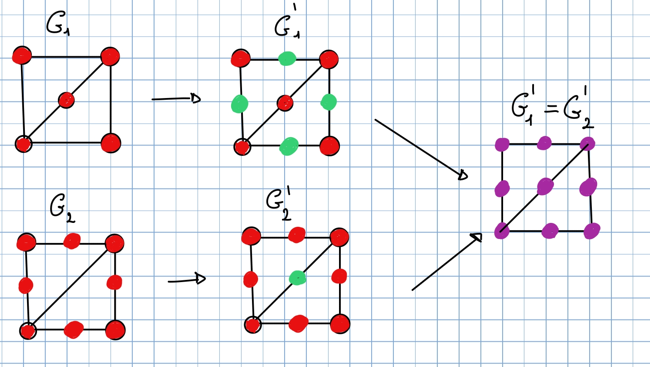 Questa stessa definizione si estende ai grafi orientati tenendo però presente la suddivisione di un arco orientato in 2 archi orientati.
Questa stessa definizione si estende ai grafi orientati tenendo però presente la suddivisione di un arco orientato in 2 archi orientati.
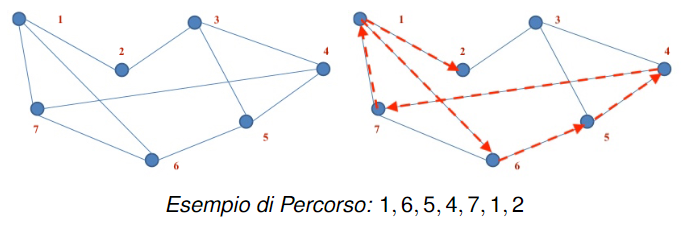
Percorso
Un percorso in un grafo è una sequenza di nodi adiacenti ossia tali che per ogni avrò una coppia che è un arco del grafo.
- il nodo è detto nodo origine
- il nodo è detto nodo destinazione
- i nodi con sono detti nodi intermedi
La lunghezza di un percorso è il numero di archi che lo compongono, ovvero
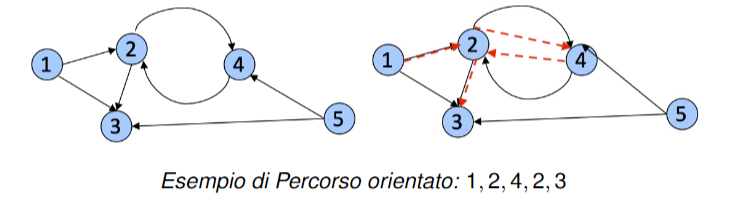
 Il percorso cambia leggermente nel caso di un grafo orientato, infatti in questo caso ogni arco si può percorrere seguendo il suo verso.
Il percorso cambia leggermente nel caso di un grafo orientato, infatti in questo caso ogni arco si può percorrere seguendo il suo verso.
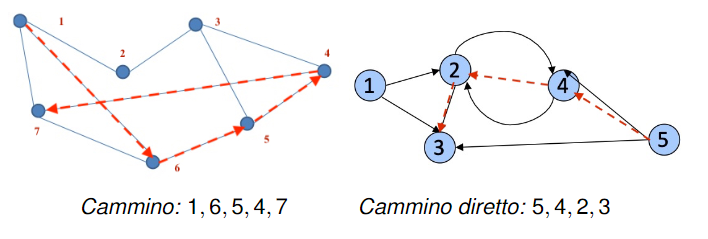
Cammino
Un percorso si dice cammino quando tutti i nodi che attraversa sono differenti.
Circuito
Un percorso si dice circuito quando è un percorso chiuso ovvero un percorso tale che
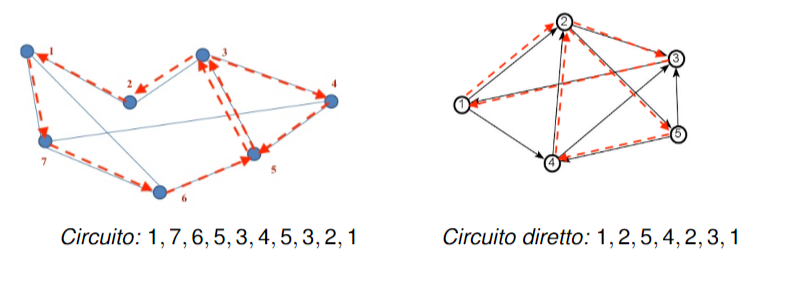
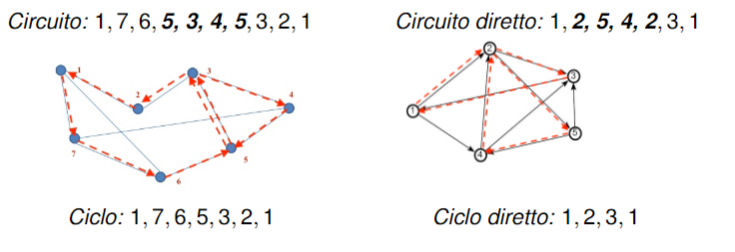
Ciclo
Un ciclo in un grafo è un circuito chiuso, ovvero un circuito dove tutti i vertici sono diversi e .
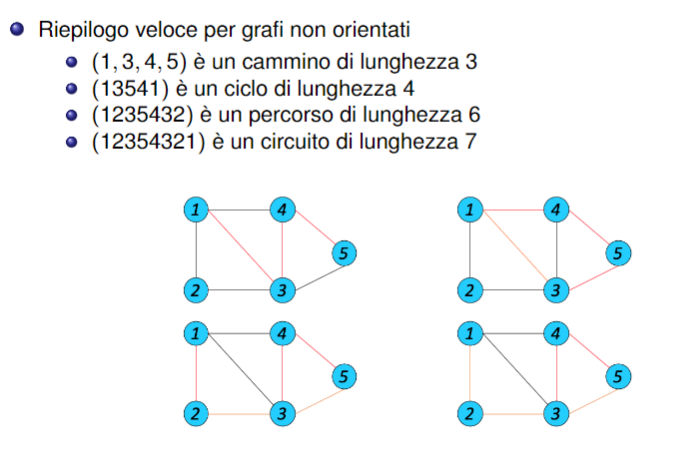
Riepilogo
SUMMARY
Cammini e cicli
Dalle spiegazioni date ne traiamo che:
- Dato un percorso da un nodo ad un nodo possiamo costruire un cammino da a
- Dato un circuito possiamo costruire un ciclo
Grafi aciclici
Un grafo si dice aciclico se non possiede cicli
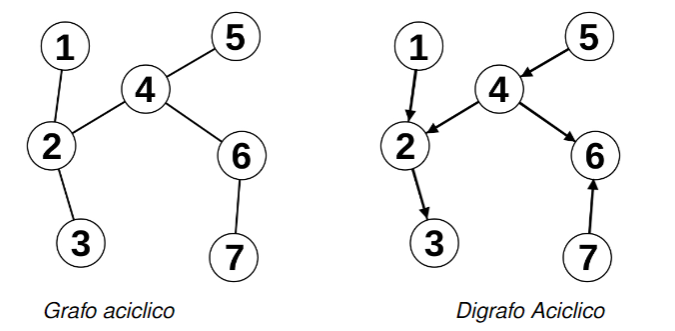 Partendo da questi due grafi è impossibile creare un ciclo
Partendo da questi due grafi è impossibile creare un ciclo
Componenti connesse
Dato un grafo diciamo che due vertici sono connessi se esiste un cammino da a
Definizione di componenti connesse^4e37c4
Sia un grafo. Consideriamo una partizione indotta dalla relazione di connessione tra i vertici che crea dei sottoinsiemi dove ciascun rappresenta un insieme di vertici connessi tra loro tramite percorsi all’interno del grafo . Per ogni sottoinsieme , definiamo il sottografo , dove è l’insieme degli archi di che collegano i vertici di . Ciascun sottografo viene detto componente connessa di .
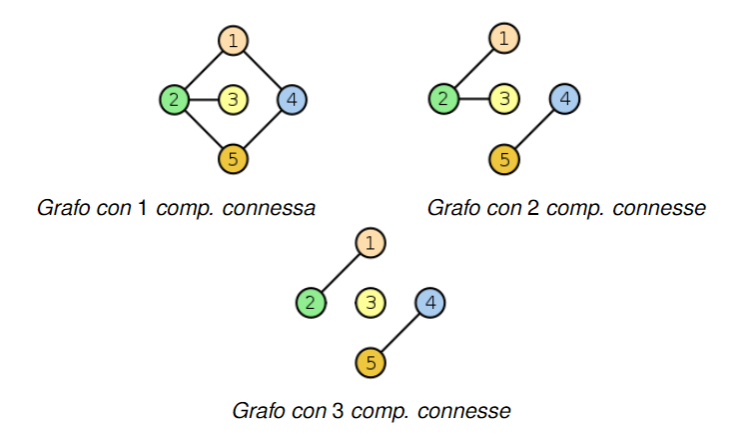
Grafo connesso
Un grafo (non orientato) si dice connesso se, per ogni coppia di vertici del grafo, esiste un percorso che li collega. In altre parole, il grafo ha una sola componente connessa, ovvero tutti i vertici appartengono alla stessa componente.
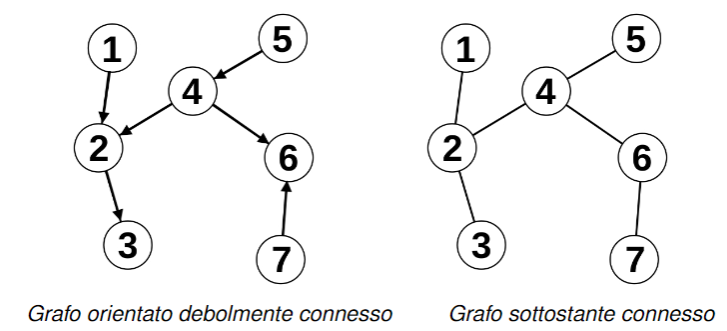
Grafo orientato debolmente connesso
Un grafo orientato di dice debolmente connesso se il grafo non orientato ottenuto eliminando da l’orientamento degli archi è connesso
Grafo sottostante
Il grafo ottenuto eliminando da un grafo orientato l’orientamento degli archi si chiama grafo sottostante
Esempio
Componenti fortemente connesse
Dato un grafo orientato , diciamo che due vertici sono fortemente connessi se esiste sia un cammino da a che un cammino da ad .
Definizione di Componenti fortemente connesse
La definizione è molto simile a questa cambia solo che la relazione viene indotta dalla relazione di connessione forte e che i sottografi finali si chiamano componenti fortemente connesse di G.
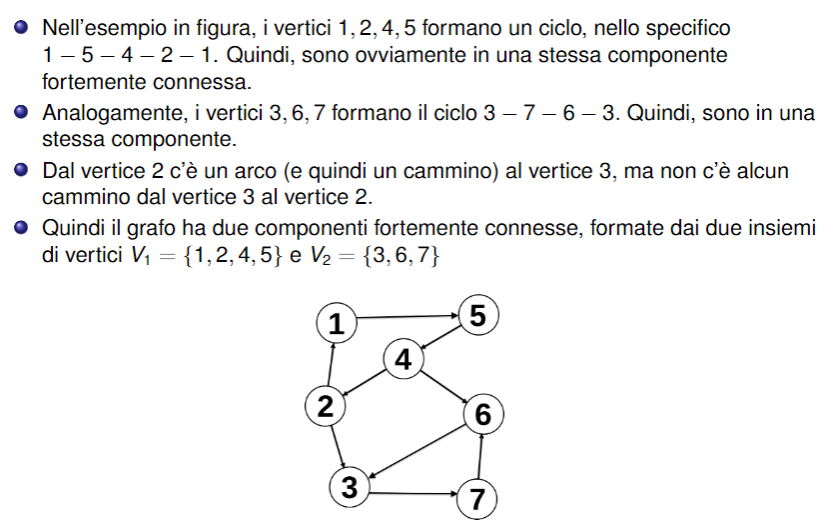
Grafo orientato fortemente connesso
Sia un grafo orientato. si dice fortemente connesso se ha una sola componente fortemente connessa.
Grafi k-connessi
Dato un grafo :
- Il grafo si dice k-connesso rispetto agli archi se dati comunque due vertici esistono cammini ad archi disgiunti tra .
- Il grafo si dice k-connesso rispetto ai vertici se dati comunque due vertici esistono k cammini a nodi disgiunti tra . Dalla definizione di k-connessione rispetto agli archi si deduce che per disconnettere il grafo è necessario rimuovere almeno k archi. Dalla definizione di k-connessione rispetto ai vertici si deduce che per disconnettere il grafo è necessario rimuovere almeno k vertici.
Rappresentazione di un grafo come matrice
Dato un grafo con . La matrice detta matrice di adiacenza del grafo ha dimensione dove è il numero di vertici, ed è formata in questo modo:
- se i vertici e sono connessi da un arco
- se i vertici e non sono connessi da un arco
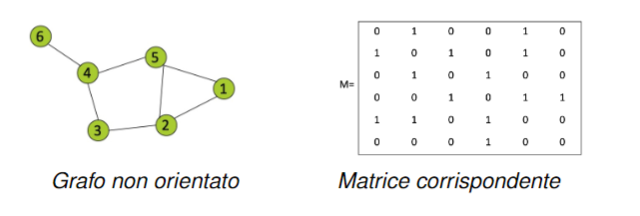
- La somma dei valori di ogni riga è il grado del vertice
- Se ci sono degli uno nella diagonale principale vuol dire che nel grafo ci sono dei cappi
- La matrice è simmetrica ovvero per ogni e : .
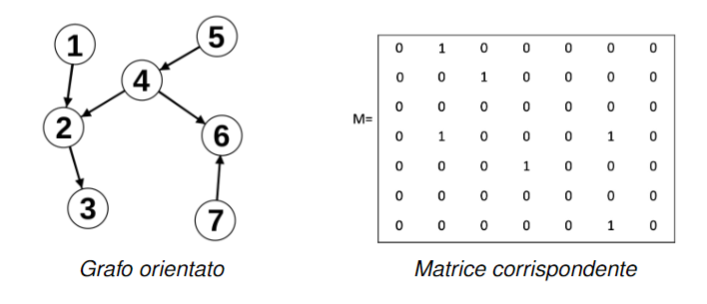
- La somma degli 1 in ogni riga è il grado in uscita del nodo corrispondente
- La somma degli 1 in ogni colonna indica il grado in entrata del nodo corrispondente
- La matrice non è simmetrica
Matrice associata alle componenti connesse
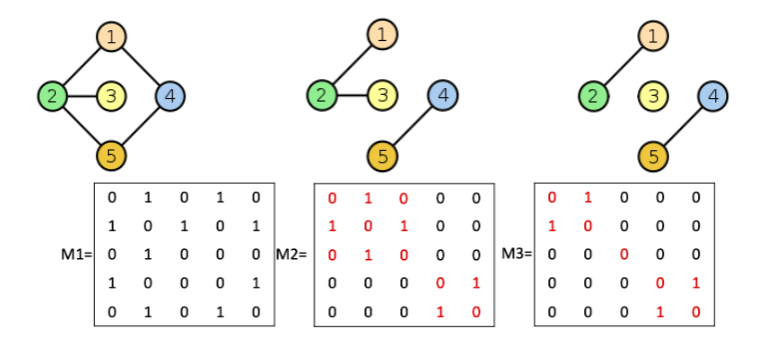 Come possiamo notare ogni componente connessa crea un blocco dove è il numero di vertici della componente.
Come possiamo notare ogni componente connessa crea un blocco dove è il numero di vertici della componente.
Cicli in un digrafo
Sia un grafo orientato per ogni vertice siano e rispettivamente il grado in uscita ed in entrata di i. Se per ogni siano > 0 e > 0 allora il grafo G contiene un ciclo Dimostrazione Dal momento che > 0 esiste un vertice tale che esiste un arco da a , stessa cosa vale per infatti siamo sicuri che esiste un arco da a , se iteriamo questo processo sino a quando non abbiamo una sequenza di vertici tali che ognuno è connesso da un arco al successivo. Se per il Pigeonhole Principle almeno 2 di questi n+1 vertici devono coincidere. Questo dimostra il teorema.
Esempio
Il grafo in figura possiede diversi cicli e, in particolare, un ciclo che coinvolge tutti i vertici: . Come si può facilmente calcolare dalla matrice di adiacenza, il grado di ogni vertice è maggiore di zero.
Inoltre possiamo dire che un grafo orientato possiede un ciclo se un suo sottoinsieme lo possiede e quindi riscrivere il teorema così. Rivisitazione del teorema per il sottografo Sia un grafo orientato. Allora possiede un ciclo se e solo se esiste un sottoinsieme , tale che il sottografo indotto verifica la seguente proprietà: per ogni vertice siano > 0 e > 0 allora ha un ciclo
Algoritmo per trovare un ciclo in un grafo
Sia la matrice del grafo, ed la matrice ottenuta da eliminando la i-esima riga e colonna, sia inoltre la dimensione della matrice (il suo numero di righe o colonne)
- Se controllando la matrice tutti i vertici del grafo hanno grado in uscita > 0 e grado in entrata > 0 terminiamo e diciamo che il grafo possiede un ciclo
- Altrimenti, prendiamo un vertice con grado di uscita/entrata = 0 e lo eliminiamo sia dalla matrice associata al grafo creando la matrice
- Ripeti passo 2-3
- Se la = 1 ci fermiamo e diciamo che il grafo è aciclico
Esempio
I successivi due passi dell’algoritmi ci fanno prima eliminare il vertice 7 che ha grado in uscita ed in ingresso entrambi uguali a 0 e poi eliminare il vertice 5 che ha grado in entrata uguale a 0. Otteniamo così il sottografo in figura che verifica la condizione del teorema e quindi possiede un ciclo.
Percorsi tra nodi
Dalle matrici matrice associata ad un grafo possiamo notare che la matrice ci dice se esiste un arco tra 2 vertici. Se volessimo cercare dei percorsi più lunghi?
Esempio
Non esiste un percorso di lunghezza 1 tra il 6 ed il 5 però ne esiste uno di lunghezza 2
TIP
Come facciamo a trovare questi percorsi più lunghi? Ci basta moltiplicare la matrice per se stessa tante volte quanto è la lunghezza del percorso che devo analizzare:
- Se voglio trovare i percorsi di lunghezza 2, mi basta moltiplicare la matrice per se stessa ()
- Se voglio trovare i percorsi di lunghezza 3, mi basta fare la matrice cubica ()
- Se voglio trovare i percorsi di lunghezza , basta fare In questo modo siamo in grado di trovare il numero di percorsi di lunghezza arbitraria per ogni coppia di nodi
Esempio
Tra i nodi 1 e 4 non esiste un percorso di lunghezza 1, però ne esiste uno di lunghezza 2
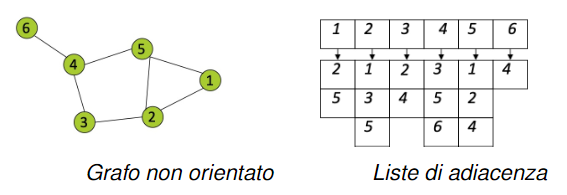
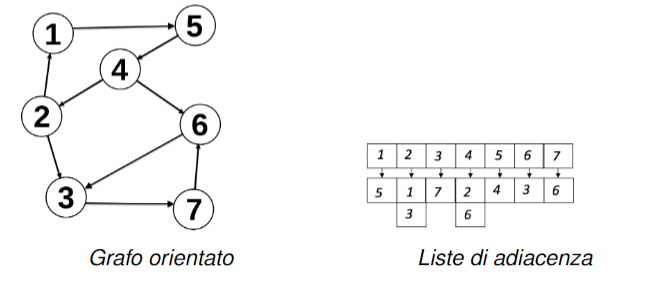
Rappresentazione di un grafo con liste di adiacenza
Un grafo può essere rappresentato pure con le liste di adiacenza, ovvero un array i cui elementi sono i nodi e per ogni nodo viene associato un altro array con la lista dei nodi collegati ad esso. Lo spazio di cui abbiamo bisogno per rappresentare un grafo con una lista di adiacenza lo calcoliamo cosi:
- Grafo non orientato:
- Grafo orientato:
Circuito Euleriano
Un circuito euleriano è un circuito chiuso che passa per ogni arco del grafo esattamente una volta. Un grafo si dice euleriano, se possiede un circuito euleriano.
Esempio
In questo grafo troviamo un circuito euleriano ovvero:
TIP
Un qualsiasi grafo è euleriano se e solo se è connesso ed i suoi vertici hanno tutti grado pari
Cammino Euleriano
Un grafo ammette un cammino euleriano se e solo se è connesso e al massimo due dei suoi vertici hanno grado dispari. In tal caso, i vertici di grado dispari rappresenteranno il punto di inizio e il punto di fine del cammino euleriano.
Esempio
Il grafo in figura ha 2 vertici di grado dispari A e C ma possiede un cammino che passa per tutti gli archi una ed una sola volta: A − B − C − D − E − A − C
Cammino Hamiltoniano
Sia un grafo (digrafo) connesso.
Un cammino hamiltoniano di è un circuito che passa una ed una sola volta per tutti i vertici di .
Se il cammino è chiuso, ovvero se è un ciclo, tale ciclo si dice ciclo Hamiltoniano. Un grafo si dice hamiltoniano, se possiede un ciclo hamiltoniano.

Esempio
Il grafo A è hamiltoniano, perché possiede il ciclo hamiltoniano
Grafi pesati
Per poter usare i grafi come strutture dati abbiamo la necessità di associargli un peso (costo, valore), questi possono essere associati agli archi, ai nodi o ad entrambi
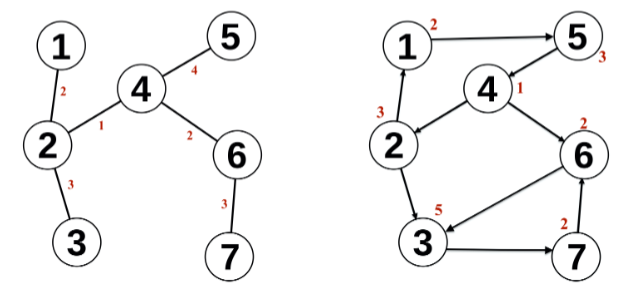 Dato un grafo pesato, il costo di un cammino può essere:
Dato un grafo pesato, il costo di un cammino può essere:
- La somma dei costi associati ai suoi archi, ovvero la somma dei costi di ogni singolo arco che attraversa.
- La somma dei costi associati ai suoi vertici, ovvero la somma dei costi di ogni singolo vertice che attraversa. Da questo ne deduciamo che ci sono cammini che più costosi di altri.
EXAMPLE
Nei grafi dell’esempio: il costo del cammino è:
- per il grafo non orientato con peso sugli archi
- per il grafo orientato con peso sui vertici:
TIP
Il cammino con il costo minimo si chiama shortest path Il cammino con il costo massimo si chiama longest path
Parliamo di cammini perché non abbiamo ripetizioni
Rappresentazione dei grafi pesati
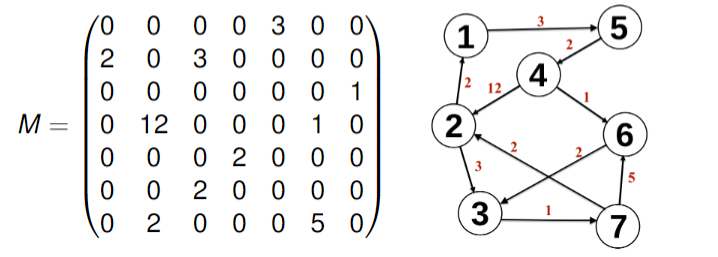
- Funzione peso sugli archi: la rappresentazione più semplice per un grafo o digrafo pesato è quella di una matrice, dove però invece di mettere 1 mettiamo il peso dell’arco, e 0 nel caso di un arco mancante.
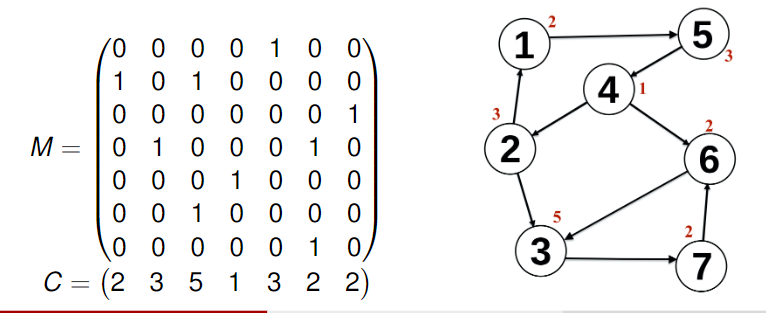
- Funzione peso sui vertici: La soluzione più semplice è creare una matrice di adiacenza e ad associargli un vettore di lunghezza con il peso di ogni vertice
Esercizio completo sui grafi
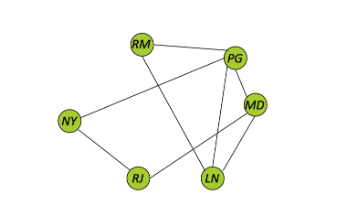
Sapendo che: Le seguenti coppie di città sono collegate da una linea aerea, che fornisce un servizio di A/R:
- Parigi-New York
- Parigi-Roma
- New York-Rio de Janeiro
- Roma-Londra
- Parigi-Londra
- Rio de Janeiro-Madrid
- Madrid-Parigi
- Madrid-Londra Rispondi alle seguenti domande:
- Qual è la strada più breve (numero di scali) da NY a Roma?
- Quella più lunga?
- Trovare (se esiste) un cammino che tocchi tutte le città, ossia un cammino hamiltoniano.
- Trovare (se esiste) un ciclo che tocchi tutte le città, ossia un ciclo hamiltoniano.
- Trovare (se esiste) un ciclo euleriano, ossia che percorre tutte le tratte una sola volta.
- Il grafo è k-connesso? Se si, qual è il valore massimo di k?
Rappresentazione del grafo:
Risposte alle domande:
- NY-PG-RM
- NY-RJ-MD-LN-PG-RM
- Si questo: NY-RJ-MD-LN-PG-RM
- RM-PG-NY-RJ-MD-LN-RM
- La trovi sotto
- Il grado minimo di ogni vertice è 2 e quindi il grafo è 2-connesso
Risposta alla domanda 5: Il Teorema di Eulero ci dice che un grafo ha un ciclo euleriano se e solo se tutti i vertici hanno grado pari. I vertici LN e MD hanno grado dispari quindi la risposta è no. Però sono solo 2 i vertici di grado dispari e quindi possiamo utilizzare l’altro teorema di Eulero che ci dice che possiamo trovare un cammino euleriano che comincia da uno dei due vertici e finisce nell’altro. Ecco il cammino: LN-PG-NY-RJ-MD-PG-RM-LN-MD
Il problema del commesso viaggiatore
Il problema del commesso viaggiatore anche conosciuto con la sigla TSP è il problema di trovare un circuito hamiltoniano che minimizza il costo totale per un grafo pesato.
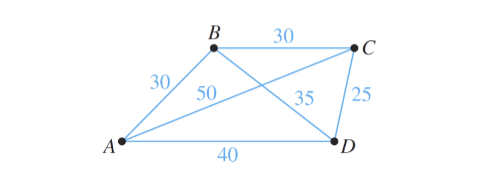 Se un commesso viaggiatore deve attraversare tutti e 4 i nodi, partendo da A e tornando ad A, qual è il percorso che minimizza il costo totale, che supponiamo, per esempio, siano distanze in KM? Possiamo risolvere il problema analizzando tutti i circuiti hamiltoniani
Se un commesso viaggiatore deve attraversare tutti e 4 i nodi, partendo da A e tornando ad A, qual è il percorso che minimizza il costo totale, che supponiamo, per esempio, siano distanze in KM? Possiamo risolvere il problema analizzando tutti i circuiti hamiltoniani
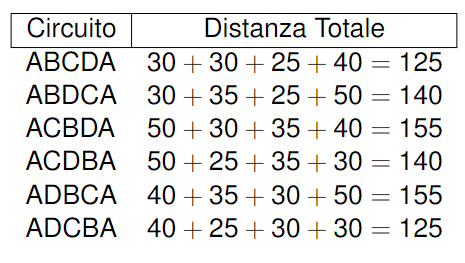 Da qui capiamo che ci sono 2 circuiti che il viaggiatore potrebbe usare. All’aumentare dei nodi da attraversare aumenta esponenzialmente il tempo di risoluzione perché si devono banalmente provare più combinazioni. Nessuno ha avuto un idea per risolvere in modo migliore, quindi resta un problema aperto.
Da qui capiamo che ci sono 2 circuiti che il viaggiatore potrebbe usare. All’aumentare dei nodi da attraversare aumenta esponenzialmente il tempo di risoluzione perché si devono banalmente provare più combinazioni. Nessuno ha avuto un idea per risolvere in modo migliore, quindi resta un problema aperto.
Grafi planari
Sia un grafo non orientato diciamo che è planare se può essere raffigurato in modo che non si abbiano archi che si intersecano.
 Teorema di Kuratowski
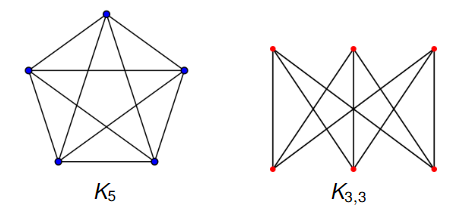
Un grafo è planare se e solo se non contiene alcun sottografo che sia omeomorfo a o a (ricordiamo i grafi bipartiti completi)
Teorema di Kuratowski
Un grafo è planare se e solo se non contiene alcun sottografo che sia omeomorfo a o a (ricordiamo i grafi bipartiti completi)
 Criteri più semplici
Se è un grafo connesso e planare se allora
oppure
Se è un grafo connesso e planare se e non ci sono cicli di lunghezza 3 allora
Criteri più semplici
Se è un grafo connesso e planare se allora
oppure
Se è un grafo connesso e planare se e non ci sono cicli di lunghezza 3 allora
Formula di Eulero
Se prendiamo un grafo planare e lo disegniamo sul piano possiamo individuare le facce ovvero il numero di regioni chiuse delimitate da archi del grafo (dobbiamo contrare anche la regione esterna, quella infinita).
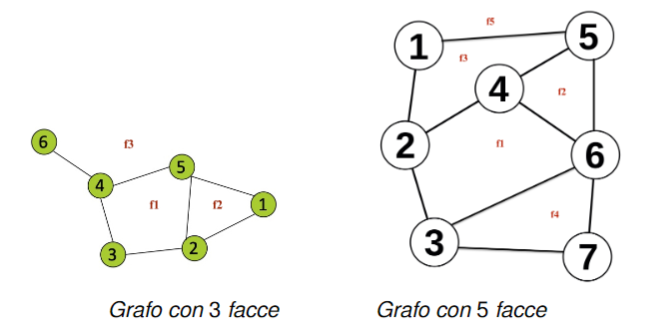
Formula di Eulero
Se indichiamo con:
- il numero di vertici
- il numero di archi
- è il numero di facce
vale la seguente formula: dalla quale possiamo ricavare le formule inverse:
Dimostrazioni vari teoremi
Teorema Sia un grafo connesso con . Supponiamo che per ogni . Allora possiede un ciclo. Dimostrazione Ordiniamo i vertici e chiamiamoli con . Partiamo da v_1 e costruiamo il cammino più lungo possibile senza ripetizioni di vertici, supponiamo che il cammino più lungo senza ripetizioni sia , dal vertice possiamo ancora raggiungere un altro vertice, dato il grado di almeno 2, dato che ci siamo fermati vuol dire che possiamo raggiungere solo un vertice già visto il che dimostra l’esistenza di un ciclo
Teorema Sia un grafo connesso e aciclico. Allora Dimostrazione Il teorema è banalmente vero se . Supponiamo allora , essendo il grafo connesso ed aciclico deve esiste un vertice di grado altrimenti il grafo avrebbe un ciclo, prendiamo questo vertice e l’arco ad esso incidente il grafo e li rimuoviamo, il grafo indotto è connesso ed aciclico altrimenti dovremmo avere 2 vertici, che sono connessi solo da un cammino passante per ma ciò implicherebbe che ha grado maggiore di e quindi per induzione ha . Aggiungendo e l’arco ad esso incidente, abbiamo quindi che
Teorema Sia un grafo planare connesso, con vertici, archi e facce. Allora Dimostrazione Se il grafo possiede un ciclo, allora togliamo uno degli archi che completa tale ciclo, il numero di archi e di facce si abbassa allora di una unità e quindi la quantità rimane invariata. Ripetiamo tali sottrazioni di archi, sino a quando non eliminiamo tutti i cicli dall’albero, a questo punto avremo un grafo connesso ed aciclico con con visto che non ci sono cicli. Quindi
Grafi planari massimali o triangolare
Un grafo planare si dice massimale (o triangolare), se è planare e se aggiungendo un nuovo arco ad una qualunque coppia di vertici il grafo non è più planare. Ogni sua faccia è racchiusa da 3 archi. Dunque un grafo planare massimale ha archi e facce.
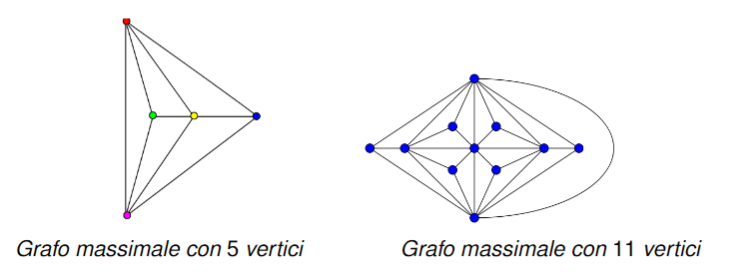
Colorazione di un grafo
Colorare un grafo vuol dire assegnare un colore ad ogni vertice in maniera tale che due vertici collegati da un arco abbiano colori distinti, un grafo è k-colorabile se è possibile colorare i suoi vertici rispettando il vincolo appena descritto usando al più colori. Il numero cromato di un grafo è denotato con
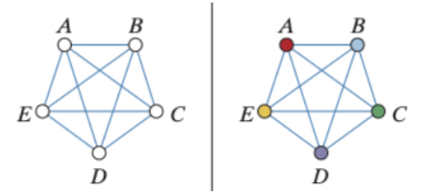
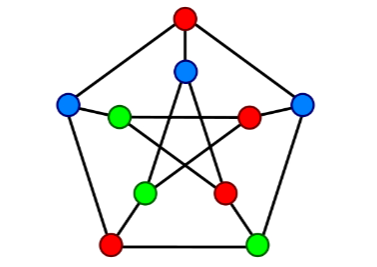 Per un grafo completo con vertici, in cui ogni nodo è collegato ad ogni altro nodo, avremo bisogno di colori distinti, in figura possiamo vedere una colorazione di
Per un grafo completo con vertici, in cui ogni nodo è collegato ad ogni altro nodo, avremo bisogno di colori distinti, in figura possiamo vedere una colorazione di
 Per un grafo bipartito basterà usare 2 colori diversi, uno per e uno per come di seguito
Per un grafo bipartito basterà usare 2 colori diversi, uno per e uno per come di seguito
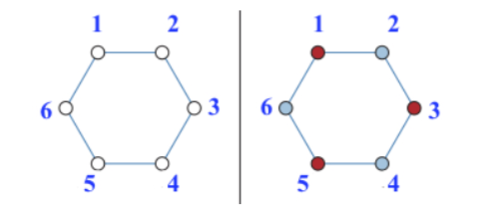
 Per un grafo con un semplice ciclo con vertici ci basterà usare:
Per un grafo con un semplice ciclo con vertici ci basterà usare:
- n pari: Possiamo usare sempre 2 colori diversi
- n dispari: Possiamo usare colori diversi
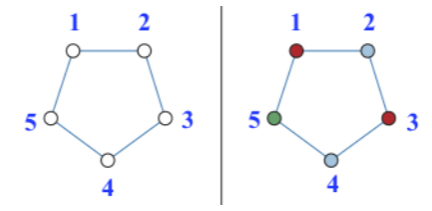
Teorema di Brooks
Una colorazione ottimale di un grafo è una colorazione dei vertici di che usa il numero minimo possibile di colori, ossia . Teorema Sia un grafo connesso con vertici i gradi dei vertici del grafo in ordine crescente. Allora Dimostrazione Il Teorema si può facilmente dimostrare per induzione. Se togliamo infatti il vertice di grado maggiore , rimaniamo con un grafo con un vertice in meno e colorabile, per ipotesi induttiva, con al più colori. Quando aggiungiamo il vertice tolto, il caso peggiore è che i vertici a lui connessi, siano tutti di colore diverso e quindi gli dobbiamo dare il colore rimasto dei .
Teorema di Brooks (versione forte)
Sia un grafo connesso con n vertici, e siano i gradi dei vertici del grafo in ordine decrescente. Se non è un grafo completo e non è un ciclo semplice con numero dispari di vertici, allora
Teorema dei 4 colori
Sia un grafo planare, allora .
Albero libero
Un albero libero (che di solito indichiamo con ) è un grafo connesso e aciclico, questo ha esattamente archi, inoltre essendo connesso ogni vertice ha grado almeno e deve esistere almeno un vertice di grado altrimenti avrebbe un ciclo.
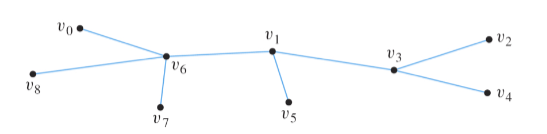
- Se ha un vertice allora questi si chiamano vertici terminali
- Se ha più di 2 vertici, i vertici di grado 1 sono detti terminali o foglie, mentre i vertici di grado maggiore di 1 sono detti vertici interni (il grafo sopra ha 6 foglie e 3 vertici interni)
Foresta
Una foresta è un insieme di uno o più alberi quindi un grafo aciclico ma non necessariamente connesso. Ogni componente connessa del grafo è un albero della foresta.
- Se ha solo 1 o 2 vertici allora tutti i vertici sono detti Terminali
- Se ha più di 2 vertici, i vertici di grado 1 sono detti foglie, mentre i vertici di grado maggiore sono detti vertici interni
Di seguito un grafo con 6 foglie e 3 nodi interni:
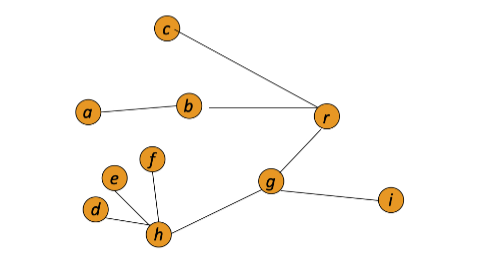
Alberi radicati
Dato un albero se scegliamo un nodo come radice e immaginiamo di impiantarlo con un chiodo, per gravità tutti gli altri nodi cadranno, così otteniamo un albero radicato
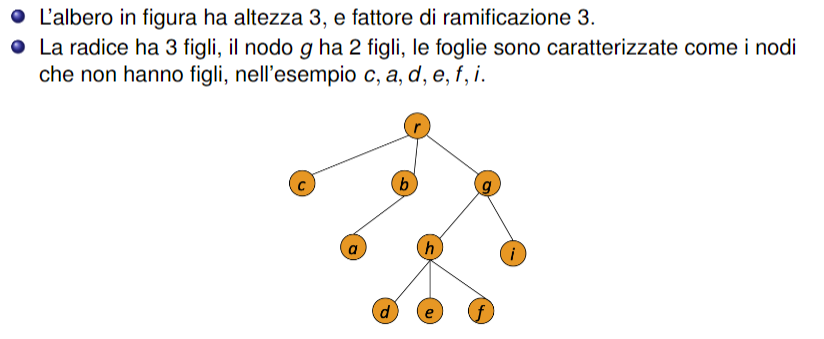
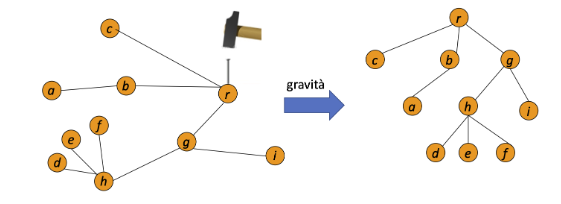 Dato un albero radicato:
Dato un albero radicato:
- l’altezza è la lunghezza del cammino più lungo
- Il fattore di ramificazione dell’albero è il numero massimo di figli che ognuno dei nodi ha
- In un albero radicato, i nodi figli di un nodo sono quelli immediatamente sottostanti a esso e direttamente collegati tramite un arco. Il nodo che li collega dall’alto è chiamato nodo padre.
Problemi combinatori sui grafi
Due problemi sui grafi che ricadono nella classe N P- hard sono:
- Il problema della colorazione di un grafo utilizzando il numero minimo di colori;
- il problema della eliminazione del numero minimo di vertici di un grafo, per renderlo aciclico.