Questo file è la rielaborazione delle slide 01_Parte1.pdf
Logica proposizionale
La logica è un linguaggio formale usato per rappresentare informazioni. Ogni linguaggio è formato da:
-
Sintassi: che definisce le frasi del linguaggio
-
Semantica: che definisce il significato delle frasi La logica più semplice di tutti è la logica proposizionale oggi basata sulla matematica booleana, quest’ultima viene detta proposizionale perché si occupa di proposizioni, più precisamente di variabili proposizionali, quest’ultime possono assumere solo 2 valori:
-
1 = VERO
-
0 = FALSO Ogni variabile proposizionale è già da se una “formula” proposizionale, ovviamente questa è una formula molto basilare. Per creare delle formule più complesse usiamo dei connettivi logici che sono i seguenti:
-
¬ (negazione): si legge “non”, e inverte il valore di verità di una proposizione. Se una proposizione è vera, la sua negazione è falsa, e viceversa. Questo connettivo logico rappresenta la porta logica NOT
-
∨ (disgiunzione logica): si legge “o”, ed è vera se almeno una delle due proposizioni è vera. Questo connettivo logico rappresenta la porta logica OR
-
∧ (congiunzione logica): si legge “e”, ed è vera se entrambe le proposizioni sono vere. Questo connettivo logico rappresenta la porta logica AND
-
⇒ (implicazione): si legge “se… allora…” o semplicemente “implica”. È falsa solo se il primo termine è vero e il secondo è falso.
-
⇔ (doppia implicazione o coimplicazione): si legge “se … e solo se …“. È vera quando entrambi i termini sono veri o entrambi falsi.
Esempi di formule (usando le variabili P e Q che sono scelte casualmente):
- ¬P = “Non P”
- Q
- P ∨ Q = “P o Q”
- P ∧ Q = “P e Q”
- P ⇒ Q = “se P allora Q”
- P ⇔ Q = P se e solo se Q
Come per le operazioni normali (somma, moltiplicazione, ecc…) anche queste hanno delle precedenze, la negazione (¬) ha la precedenza su tutto mentre congiunzione (∨) e disgiunzione (∧) hanno la stessa priorità infatti:
- ¬p ∨ q è la formula dove la negazione si applica solo a p
- ¬(p ∨ q) è la formula dove la negazione si applica alla disgiunzione p ∨ q
Date 2 formule e che ovviamente posso assumere solo una valore (questa cosa la impone una funzione chiamata interpretazione che appunto assegna a e i valori 1 o 0) Di seguito si calcola il valore di verità delle seguenti formule:
- I(¬) è vera solo se è falsa
- I( ∨ ) è vera se almeno una tra o è vera
- I( ∧ ) è vera se entrambe sono vere
- I( ⇒ ) è falsa solo quando è vera e è falsa, nei restanti casi è vera
- I( ⇔ ) è vera se e solo se == Questa è la tabella della verità di tutte queste formule:
| ¬ | ∨ | ∧ | ⇒ | ⇔ | ||
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Nomenclature varie:
- Data una formula diremo che è ==soddisfacibile== se esiste almeno un caso in cui sia vera, qualunque siano i valori delle variabili.
- Data una formula diremo che è insoddisfacibile se non esiste almeno una caso in cui sia vera, qualunque siano i valori delle variabili.
- Data una formula si dice tautologia se è sempre vera qualunque siano i valori delle variabili.
Di seguito degli esempi (usando le variabili della tabella di verità):
- ∧ è soddisfacibile
- ∨ ¬ è tautologia (Questo viene chiamato ==Principio del terzo escluso==)
- ∧ ¬ è insoddisfacibile (Questo viene chiamato ==Principio di non contraddizione==)
Due formule e si dicono equivalenti se hanno lo stesso valore, questo concetto in simboli lo esprimiamo così:
Per la disgiunzione e la congiunzione vale la proprietà commutativa e associativa
- p ∨ q ≡ q ∨ p (commutativa della disgiunzione)
- p ∨ (q ∨ r ) ≡ (p ∨ q) ∨ r (associatività della disgiunzione)
Giustificazione o conseguenza logica:
Sia un insieme di proposizioni e una proposizione generica, ci chiediamo quando giustifica questa domanda la denotiamo con: |=
Di seguito un esempio:
= { p, p ⇒ q }
|=
Questa è la tavola di verità dell’esempio
 N.B: Per essere vero che giustifica tutte le formule di devono essere vere e anche deve essere vera. Questa cosa si capisce ancora meglio in questo esempio
N.B: Per essere vero che giustifica tutte le formule di devono essere vere e anche deve essere vera. Questa cosa si capisce ancora meglio in questo esempio
= { p ∨ r, q ∨ ¬r }
|= p ∨ q
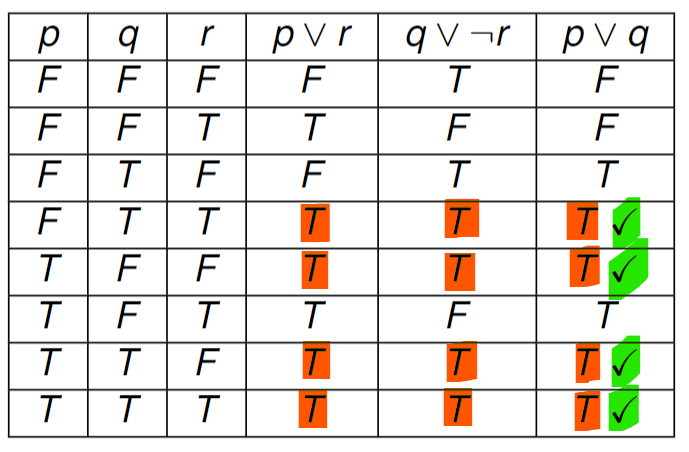
Come possiamo facilmente notare P giustifica quella disgiunzione (ovvero p ∨ q) solo quando tutte le formule di e la disgiunzione tra e sono vere (attenzione ai vari casi nella tabella).
TIPS: Come creare tutte le combinazioni tra le variabili senza confondersi
Altre equivalenze logiche
- (eliminazione della doppia implicazione)
- (eliminazione dell’implicazione)
- distributività della congiunzione sulla disgiunzione
- distributività della disgiunzione sulla congiunzione
TIPS: Come distribuire le congiunzioni sulle disgiunzioni e viceversa
Molte volte formule complesse vengono standardizzate in 2 forme chiamate “normali”:
- CNF (Forma Normale Congiuntiva) che si basa sul fare un AND di vari OR:
- (p ∨ q) ∧ (¬p ∨ ¬r ∨ s)
- DNF (Forma Normale Disgiuntiva) che si basa sul fare un OR di vari AND:
- (p ∧ q) ∨ (¬p ∧ ¬r ∧ s)
Una qualunque formala si può trasformare in una delle 2 forme normali sopracitate, questo si fa seguendo questi step:
- Elimina le coimplicazioni p ⇔ q dalla formula sostituendole con (p ⇒ q) ∧ (q ⇒ p)
- Elimina le implicazioni p ⇒ q dalla formula sostituendole con ¬p ∨ q
- Sposta le negazioni a ridosso delle variabili proposizionali ed elimina le doppie negazioni.
- ¬(¬p ∨ ¬r ∨ s) diventa (p ∧ r ∧ ¬s) (Veridicità di questa cosa)
- Di questo step abbiamo 2 casi:
- Per costruire una CNF distribuiamo le congiunzioni sulle disgiunzioni, di seguito un’esempio:
- Scrivo entrambe le variabili separate con l’operatore logico che trovo tra le parentesi
- Sostituisco la seconda parentesi ai puntini
- distribuisco p e q sulla parentesi
- elimino la formula perché sarebbe sempre falsa
- Per costruire una DNF distribuiamo le disgiunzioni sulle congiunzioni, di seguito un’esempio
- Prendo una variabile della prima parentesi, gli metto vicino l’operatore logico fuori dalla parentesi, faccio questa cosa una volta per ogni variabile della della seconda parentesi. Il segno che c’è tra le nuove parentesi e quello dentro la parentesi iniziale.
- Sostituisco ogni variabile della seconda parentesi iniziale ai puntini
- elimino la formula perché sarebbe sempre falsa
Per fare questa cosa in modo più veloce esiste ✨metodo Di Bella ✨
Esempio:

- Per costruire una CNF distribuiamo le congiunzioni sulle disgiunzioni, di seguito un’esempio:
Insiemi
Gli insiemi vengono considerati una collezione ben definita di oggetti.
- Per esprimere l’appartenenza ad un insieme usiamo la seguente espressione:
- x ∈ T (x è un elemento generico e T è un’insieme generico)
- Per esprimere la non appartenenza ad un’insieme usiamo la seguente espressione:
- Dato che un’insieme è univocamente caratterizzato dal suo contenuto, 2 insiemi si dicono uguali se hanno gli stessi elementi, in simboli sarebbe:
- A = B ⇔ (∀x)(x ∈ A ⇔ x ∈ B) (A è uguale a B se e solo se qualsiasi x che appartiene ad A appartiene anche a B)
- A = {1, 2, 3} e B = {2, 3, 1, 2, 3} sono uguali perché contengono gli stessi elementi.
Per specificare un’insieme è sufficiente elencarne gli elementi, in questo modo:
- T = {1,2,3} (T è un'insieme contente i numeri 1,2,3) Più in generale possiamo specificare un’insieme esprimendo la proprietà che caratterizza i suoi elementi. Supponiamo che sia la proprietà di essere un divisore di 100 allora (con questa nomenclatura indichiamo un’insieme di tutti gli elementi che rendono vera la proprietà ) è un insieme. Per poter esprimere un’insieme sotto questa forma la proprietà deve essere ben definita ovvero che per ogni valore di , può assumere solo 2 valori vero o falso, di seguito un esempio di non insieme:
- Supponiamo sia la proprietà di essere “alti”, allora non è un insieme. In questo caso parliamo di un non-insieme perché la proprietà di essere alti non è una proprietà ben definita in termini matematici infatti è una nozione che può variare in base al contesto.
Cardinalità
Si dice Cardinalità il numero di elementi che costituisce un’insieme e si denota con il simbolo: questo potrebbe assumere anche il valore di , un’esempio potrebbe essere l’insieme dei numeri pari che ha una cardinalità uguale ad .
Nomenclature:
- Per indicare un’insieme costituito da un solo elemento usiamola parola singoletto
- invece per indicare un’insieme vuoto usiamo il seguente simbolo:
- ∅ (la cardinalità del seguente insieme è uguale a 0)
Sottoinsieme e sovrainsieme
Se abbiamo 2 insiemi A e B, e tutti gli elementi di A appartengono a B, diciamo che A è un sottoinsieme di B e lo denotiamo così:
- A ⊆ B ⇔ (∀x)(x ∈ A ⇒ x ∈ B) (A è un sottoinsieme di B se e solo se qualunque x che appartiene ad A, appartiene anche a B) facendo rifermento allo stesso caso potremmo dire che B è un sovrainsieme di A e lo denotiamo così:
- B ⊇ A ⇔ (∀x)(x ∈ A ⇒ x ∈ B) (A è un sovrainsieme di B se e solo se qualunque x che appartiene ad A, appartiene anche a B)
Nota bene tra le due espressioni scritte qua sopra cambia la direzione del segno
Le relazioni A ⊆ B è verificata anche nel caso A = B, se volessimo esprimere il concetto A ⊆ B ma specificando che A è diverso da B (quindi che in B ci sono elementi che in A non ci sono) scriviamo in questo modo A ⊂ B, in questo caso diciamo che A è un sottoinsieme proprio di B (tutta questa affermazione vale anche per il sovrainsieme).
Anche in questo caso possiamo definire un sottoinsieme definendo la proprietà che caratterizza ogni singolo elemento. Supponendo che sia un insieme, è un sottoinsieme definito in questo modo:
- = { e } (==ogni elemento del sottoinsieme deve appartenere sia a sia rispettare la proprietà ==)
- è l’insieme dei numeri interi positivi da 1 a 100, la proprietà per essere vera un numero deve essere multiplo di 10. Allora un sottoinsieme definito cosi: { e } sarà uguale {10, 20, 30, 40, 50, 60, 70, 80, 90, 100}.
Un’insieme si dice discreto se è possibile ordinare i suoi elementi in maniera tale che tra un qualunque elemento è il suo successivo non ci siano altri elementi. Ricordando:
- N = {0, 1, 2, 3, 4, …} è un insieme discreto
- Z = {… , −4, −3, −2, −1, 0, 1, 2, 3, 4, …} è un insieme discreto
- Q = { : n, m ∈ Z} non è un’insieme discreto
- R = {x : x razionale o irrazionale } non è un insieme discreto
Operazioni tra insiemi
Le operazioni principali tra insiemi sono:
- Unione di 2 insiemi A e B, è l’insieme formato da quegli elementi che appartengono ad almeno uno dei due. La notazione che usiamo è la seguente:
- ∪ = { : oppure .} (A unito B è formato da qualsiasi x che appartiene ad A oppure a B)
- Se = {1, 2, 3} e = {3, 4, 5} allora = {1, 2, 3, 4, 5}. L’elemento 3, presente in entrambi gli insiemi, è presente nell’unione una sola volta.
- ∪ = { : oppure .} (A unito B è formato da qualsiasi x che appartiene ad A oppure a B)
- Intersezione di 2 insiemi A e B, è l’insieme formato dagli elementi che appartengono ad entrambi gli insiemi. La notazione che usiamo è la seguente:
- = { : e .} (== intersezione è formata dalle x che appartengono sia ad che a ==)
- Se A = {1, 2, 3} e B = {3, 4, 5} allora A ∩ B = {3} notiamo che l’elemento 3, è l’unico presente in entrambi gli insiemi
- A ∩ B = ∅. Se l’intersezione tra 2 insiemi è vuota si dicono disgiunti
- = { : e .} (== intersezione è formata dalle x che appartengono sia ad che a ==)
- Differenza di 2 insiemi, è l’insieme formato da quegli elementi del primo insieme che non appartengono al secondo insieme. La notazione che usiamo è la seguente:
- = {x : x ∈ A e .} (A differenza B è formato dalle x che appartengono ad A ma non appartengono a B)
- Altre operazioni tra insiemi Sia per l’unione che per l’intersezione valgono le proprietà commutativa e associativa
La cardinalità dell’unione di due insiemi è la somma delle cardinalità meno la cardinalità dell’intersezione. La notazione scritta sarebbe:
- = + − La cardinalità della differenza tra 2 insiemi è la differenza tra la cardinalità del primo insieme e la cardinalità dell’intersezione tra i 2 insiemi. La notazione scritta sarebbe:
- || = −
Una rappresentazione classica delle relazioni tra insiemi è il diagramma di Venn
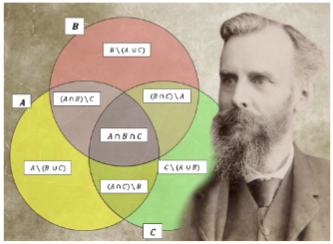 Come possiamo notare ci sono 8 regioni e sono le seguenti:
Come possiamo notare ci sono 8 regioni e sono le seguenti:
- A \ (B ∪ C)
- B \ (A ∪ C)
- C \ (A ∪ B)
- (A ∩ B) \ C
- (A ∩ C) \ B
- (B ∩ C) \ A
- A ∩ B ∩ C Un’altra regione è quella dove ci sono tutti gli elementi che non appartengono a nessuno dei 3 insiemi. Il numero di regioni nel diagramma di Venn è dove è il numero di insiemi presi in considerazione.
Altre operazioni tra insiemi
- Complemento di un’insieme, se assumiamo che tutti gli insiemi siano sottoinsiemi di un insieme “universo” detto allora viene detto complemento di A (in notazione matematica si scrive così: )
- Se A = {1, 2, 3} e U = {1, 2, 3, · · · , 10}| allora AC = {4, 5, · · · , 10} Questo tipo di operazione ha delle proprietà:
- = (il complemento del complemento di un'insieme è l'insieme stesso)
- (De Morgan: il complemento dell'intersezione è l'unione dei complementi)
- (De Morgan: il complemento dell'unione è l'intersezione dei complementi) La cardinalità di un complemento di un insieme si basa sulla cardinalità di U se U è finito allora || = |U| - |A|.
- Differenza simmetrica di 2 insiemi, è l’unione tra la differenza tra gli insiemi e quindi tutti quegli elementi del primo o del secondo che non appartengono ad entrambi. La notazione che usiamo è la seguente:
- = (A \ B) ∪ (B \ A).
- Se A = {1, 2, 3} e B = {3, 4, 5}| allora A∆B = {1, 2, 4, 5} Questo tipo di operazione ha delle proprietà:
- Commutativa: =
- Associativa: =
- =
- = (A \ B) ∪ (B \ A).
Dimostrazione diretta
Tutte le dimostrazioni di proprietà e le soluzioni di esercizi su insiemi includeranno dimostrazioni del tipo:
- dimostra che A ⊆ B o, equivalentemente, B ⊇ A,
- Per dimostrare che A ⊆ B si considera un elemento generico x ∈ A e si dimostra che x ∈ B.
- dimostra che A = B
- Per dimostrare che A = B, dobbiamo dimostrare che hanno gli stessi elementi. Quindi si dimostra che A ⊆ B e B ⊆ A.
- dimostra che A = ∅
- Per dimostrare che A = ∅ si fa vedere che la definizione di appartenenza ad A porta ad una contraddizione.
Supponiamo di avere l’insieme A definito come: A = {x ∈ N | x è pari e x è dispari} Vogliamo dimostrare che A è vuoto.
- Assumiamo il contrario: Supponiamo che esista un elemento x in A.
- Cerchiamo una contraddizione: Se x è in A, allora x è sia pari che dispari. Ma un numero non può essere contemporaneamente pari e dispari. Questa è una contraddizione.
- Conclusione: Poiché abbiamo trovato una contraddizione, l’assunzione iniziale (che esiste un elemento in A) deve essere falsa. Quindi, A è vuoto.
Insieme delle parti
Dato un’insieme T, consideriamo insieme delle parti di T un’insieme che contiene tutti i sottoinsiemi di T, lo indichiamo così:
- oppure
- Sia = {1, 2, 3} allora = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}} Cardinalità dell’insieme delle parti:
- Se = ∅ allora = {∅}
- Se = 1 quindi = {a} allora = { ∅ , {a} } = 2 elementi
- Se = 2 quindi = {a, b} allora = { ∅ , {a}, {b}, {ab} } = 4 elementi
- Se = 3 quindi = {a, b, c} allora = 8 elementi Come possiamo ben notare la cardinalità di = dove è il numero di elementi di T Proprietà: (Per capire le proprietà di consiglia prima di vedere bene:spiegazione ⊂ e ⊃)
-
- Dimostrazione: Per dimostrare che è vera l’equivalenza dobbiamo dimostrare 2 casi
- Caso ⊂: supponendo che e quindi che e da questo capiamo facilmente che e e quindi che
- Caso ⊃: supponiamo che e quindi che e quindi ciò implica che
- Dimostrazione: Per dimostrare che è vera l’equivalenza dobbiamo dimostrare 2 casi
-
- Dimostrazione: Per dimostrare questa formula dobbiamo dimostrare che ma anche che un generico elemento di non appartenga a
- Caso ⊃: Supponiamo che , allora oppure .Nel primo caso mentre nel secondo caso . In entrambi i casi, quindi, da cui .
- Caso : Sia A = {1, 2} e B = {1, 3}. L’insieme = {1, 2, 3} appartiene a ma non appartiene a ∪ ( ricordiamo che P(A) = { ∅, {1}, {2}, {1,2} } invece P(B) = { ∅, {1}, {3}, {1,3} } )
- Dimostrazione: Per dimostrare questa formula dobbiamo dimostrare che ma anche che un generico elemento di non appartenga a
Famiglia
Un insieme di insiemi, come ad esempio l’insieme delle parti, è anche detto “famiglia di insiemi”
Diagramma di Venn di famiglie di insiemi
Data una famiglia di n insiemi detta F, le regioni del diagramma di Venn sono . Una famiglia di insiemi con un numero infinito di elementi è una famiglia infinita. Se invece ha un numero finito di elementi allora è una famiglia infinita.
- Sia = {P, D} dove P è l’insieme dei numeri pari (infinito) e D è l’insieme dei numeri dispari (infinito). La famiglia F è una famiglia finita di insiemi.
- Sia = {, , , …} dove = {, · · · , }. La famiglia è infinita, ma tutti i suoi elementi sono insiemi finiti. Le operazioni di unione ed intersezione si possono estendere alle famiglie infinite.
Sia una famiglia qualunque di insiemi si indica con: l’insieme degli elementi di che appartengono ad F e viene detto insieme unione della famiglia . Quindi:
- e L’insieme unione della famiglia è uguale all’insieme di tutte le appartenenti a che rispettano la condizione che esista ed appartenga ad . ==Tutto ciò si traduce nel dire che l’insieme unione della famiglia è uguale all’unione tra tutti gli insiemi appartenenti a stesso e quindi da tutti gli elementi degli insiemi (ripetuti una volta sola)==
- Esempio:
- La famiglia di insiemi : Rappresenta tutti gli studenti di una scuola, divisi per classe. Ogni classe è un insieme di studenti.
- L’insieme : Rappresenta una singola classe.
- L’elemento : Rappresenta un singolo studente.
- L’espressione: In questo caso significherebbe “Se prendi tutti gli studenti da tutte le classi e li metti insieme, otterrai l’insieme di tutti gli studenti della scuola.” Sia una famiglia qualunque di insiemi si indica con l’insieme degli elementi che appartengono a tutti gli insiemi che appartengono ad e viene detto insieme intersezione della famiglia . Quindi:
- L’insieme intersezione della famiglia è uguale all’insieme di tutti gli elementi tali che per ogni appartenente a F, x appartiene a X. Tutto ciò si traduce nel dire che l'insieme intersezione della famiglia F è uguale all'intersezione tra tutti gli insiemi appartenenti a F stesso e quindi avremo come risultato un insieme fatto dagli elementi comuni a tutti gli insiemi.
Insiemi chiusi
Sia dato un insieme ed un operazione, se quest’ultima può essere definita o completata in allora possiamo dire che e chiuso rispetto a quell’operazione
- Sia e l’operazione che consideriamo è la somma, allora possiamo dire che U è un’insieme chiuso rispetto alla somma (la somma di 2 qualsiasi valori ci da un valore positivo e quindi che appartiene a )
- Sia e l’operazione che consideriamo è la sottrazione, allora possiamo dire che U non è un’insieme chiuso rispetto alla sottrazione (la sottrazione di 2 qualsiasi valori ci potrebbe dare un valore negativo che non appartiene )
Chiusura rispetto all’unione ed intersezione
Sia una famiglia di insiemi
- diciamo che è chiusa rispetto all’unione se per ogni coppia di insiemi e appartenenti a anche appartiene a .
- diciamo che è chiusa rispetto all’intersezione se per ogni coppia di insiemi e appartenenti a anche appartiene a .
- Sia F = { {1, 2, 3}, {1, 2}, {1, 3} } abbiamo che è chiuso rispetto all’unione ma non è chiuso rispetto all’intersezione, perché {1, 2 } ∩ {1, 3} = {1} che non appartiene ad F. Considerando una famiglia di insiemi composta da sotto insiemi di un insieme universo detto , possiamo dire che per ogni X ∈ il complemento di X rispetto ad U ovvero appartiene ad a . Quindi possiamo dire che è una famiglia di insiemi dove ogni insieme viene complementato rispetto ad
- = {1, 2, 3}
- pow()=
- = {{1}, {2, 3}, {1, 2}}
- = { {2,3}, {1}, {3} } la famiglia complemento viene definita cosi:
- = { : ∈ } ovvero come l’insieme di tutti le ∈ però complementate.
Teoremi:
- La famiglia è chiusa rispetto all’unione se e solo se la famiglia è chiusa rispetto all’intersezione.
- La famiglia è chiusa rispetto all’intersezione se e solo se la famiglia è chiusa rispetto all’unione.

Sia data:
- una famiglia finita di insiemi su un insieme
-
- una generica operazione sull’insieme
Definiamo chiusura di rispetto ad * la più piccola famiglia che contiene ed è chiusa rispetto a * .
- Esempio: sia data = {{1, 2, 3}, {1, 2}, {1, 3}, {2, 4}} ovvero famiglia non chiusa rispetto all’operazione di unione. La famiglia più piccola che contiene ed è chiusa rispetto all’operazione di unione è la famiglia = {{1, 2, 3}, {1, 2}, {1, 3}, {2, 4}, {1, 2, 3, 4}, {1, 2, 4}} intersezione
Partizioni
Una famiglia di insiemi formata da sottoinsiemi dell’insieme universo può essere chiamata anche partizione di
- Sia = {1,2,3,4,5,6,7,8,9,10,11,12} = { {1, 3, 5, 7, 8, 10, 12}, {2}, {4, 6, 9, 11} }, è una partizione di
Coppie ordinate
Consideriamo 2 elementi x e y. Creiamo una coppia ordinata dove il primo elemento è x ed il secondo elemento è y. Denotiamo tale coppia con (x, y).
- la coppia (x, y) è diversa dalla coppia (y, x) (a meno che x = y).
- (x, y) = (x′, y′) se e solo se x = x′ e y = y′
Nota
la coppia (x, y) è diversa dall’insieme {x, y} costituito dagli elementi x e y
Insieme prodotto
Dati 2 insiemi non vuoti e , l’insieme prodotto da per (che indichiamo con ) è l’insieme di tutte le coppie ordinate con e
- A × B = {(x, y) : x ∈ A e y ∈ B} A×B è l’insieme di tutte le coppie con che appartiene ad e che appartiene a
- Un’esempio di questo prodotto è il piano cartesiano che definiamo come che è un insieme formato da tutte le coppie ordinate di numeri reali.
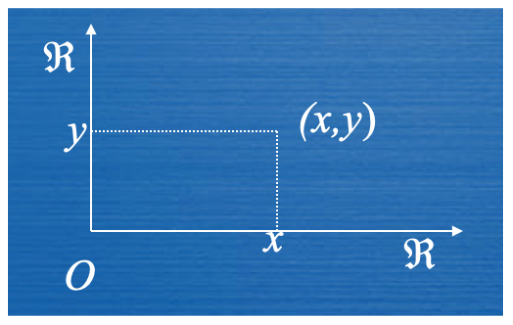
- Dati, in un certo ordine, tre insiemi A, B, C, si chiama loro prodotto, e si indica con A × B × C l’insieme di tutte le terne ordinate (x, y, z) con x ∈ A, y ∈ B, z ∈ C.
- Un’esempio di questo prodotto è il piano cartesiano che definiamo come che è un insieme formato da tutte le coppie ordinate di numeri reali.
Paradosso di Russell
Partendo dal concetto di insieme, possiamo benissimo costruire un insieme formato da tutti quegli elementi che non appartengono a se stessi e lo definiamo in questo modo:
- è l’insieme di tutti gli insiemi che non appartengono a se stessi. Per esempio, l’insieme di tutti i frutti non è un frutto, quindi potrebbe appartenere a . Usando questa definizione S ∈ S?
- Se diciamo SI: Se S appartiene a se stesso, allora per definizione di S, S non dovrebbe appartenere a se stesso (perché S contiene solo insiemi che non appartengono a se stessi). Questo è una contraddizione.
- Se diciamo NO: Se S non appartiene a se stesso, allora per definizione di S, S dovrebbe appartenere a se stesso (perché S contiene tutti gli insiemi che non appartengono a se stessi). Anche in questo caso abbiamo una contraddizione. Evitiamo questa contraddizione imponendo nella definizione dell’insieme che quest’ultimo deve essere sottoinsieme di un’insieme conosciuto, la nuova definizione di diventa: Con questa nuova definizione, il paradosso svanisce. Se proviamo a chiedere se S appartiene a se stesso, ci rendiamo conto che S è un sottoinsieme di U, ma non possiamo dire con certezza se S appartiene o meno a U. In questo modo, evitiamo il circolo vizioso che portava alla contraddizione.
Relazioni e funzioni
Relazioni
Sia un insieme non vuoto. Con il termine relazione indichiamo un insieme formato in questo modo: (per capire meglio questo insieme guarda: Insieme prodotto)
- ovvero cioè un insieme formato da tutte le coppie che rendono vera la relazione, questo insieme viene chiamato grafico della relazione
- Considera l’insieme U = {1, 2, 3}. Una possibile relazione R su U potrebbe essere “è minore di”. In questo caso, il grafico di R sarebbe {(1, 2), (1, 3), (2, 3)}, perché 1 è minore di 2 e 3, e 2 è minore di 3, questi sono gli unici 3 casi che rendono vera la relazione “è minore di”. Proprietà delle relazioni
Funzioni
Una relazione f definita su si dice funzione di (dominio) in (codominio), se per ogni esiste uno ed uno solo tale che . La notazione classica per esprimere f è la seguente: per ogni x ∈ A l’unico elemento tale che (x, y) ∈ si indica con
Casi particolari:
- per ogni x, f(x) = si dice ==applicazione identica== di
- tale che per ogni = si dice ==proiezione canonica== su .
- tale che per ogni = si dice ==proiezione canonica== su .
Dato e anche un sottoinsieme di A chiamato X si dice immagine di X il sottoinsieme di B costituito dagli elementi che provengono da X. Questo insieme si indica con f(X) e anche con la seguente definizione:
- L'immagine di X è l'insieme di tutti gli y appartenenti a B tali che esiste un x appartenente a X per cui f(x) è uguale a y si dirà immagine dell’applicazione f, ovvero tutti i possibili valori che la funzione può assumere.
Funzione iniettiva
Data un’applicazione : → se porta punti distinti del dominio su su punti distinti del codominio la funzione si dice ==iniettiva== formalmente la definiamo così:
- Per tutti x e y appartenenti ad A se x è diverso da y allora f(x) è diverso da f(y). Questo tipo di funzione viene definita funzione “uno a uno” appunto perché associa ad ogni elemento di B(codominio) soltanto un elemento di A(dominio)
- Esempio:
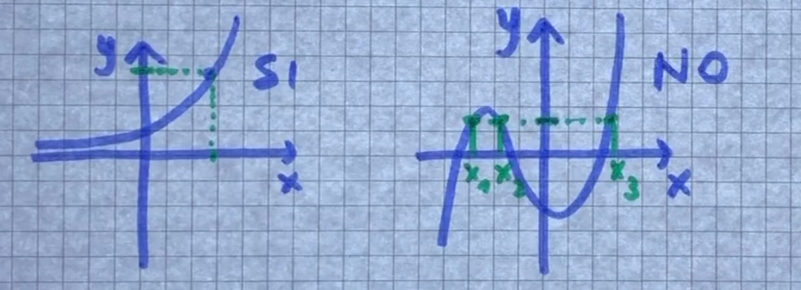
- è l’insieme delle del piano cartesiano corrisponde a nella definizione precedente
- è l’insieme delle del piano cartesiano corrisponde a nella definizione precedente
- nel primo grafico ad ogni valore di posso sempre associare un solo elemento di e quindi è iniettiva, nel secondo invece ad ogni valore di posso associare più elementi di
Funzione surgettiva
Data un’applicazione : → se l’immagine la funzione si dice ==surgettiva== ovvero un funzione che associa ad ogni elemento di B (codominio) almeno un’elemento di A(dominio).
- Esempio:
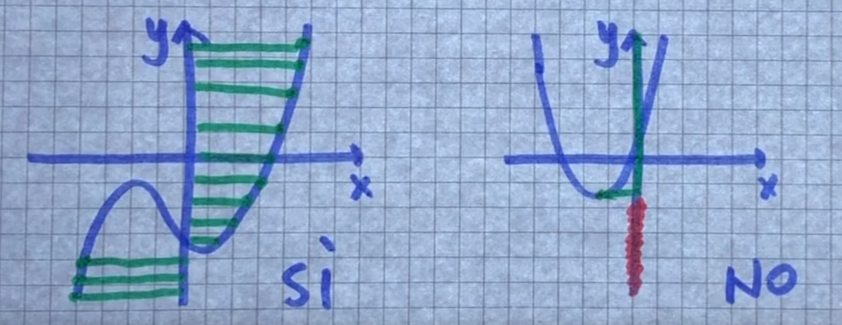
- è l’insieme delle del piano cartesiano corrisponde al dominio
- è l’insieme delle del piano cartesiano corrisponde al codominio
- nel primo grafico ad ogni valore di posso associare almeno un elemento di , nel secondo grafico invece ad ogni valore di non posso associare un valore di (dove c’è la linea rossa non posso associare a nessuna ).
Nota
- Una funzione iniettiva può avere elementi del codominio che non vengono raggiunti.
- Una funzione suriettiva, invece, raggiunge tutti gli elementi del codominio.
Funzione biiettiva
Data un’applicazione : → si dice biiettiva se è sia iniettiva che surgettiva. Questo tipo di funzione associa sempre ogni elemento di A ad ogni elemento di B
Esempio: 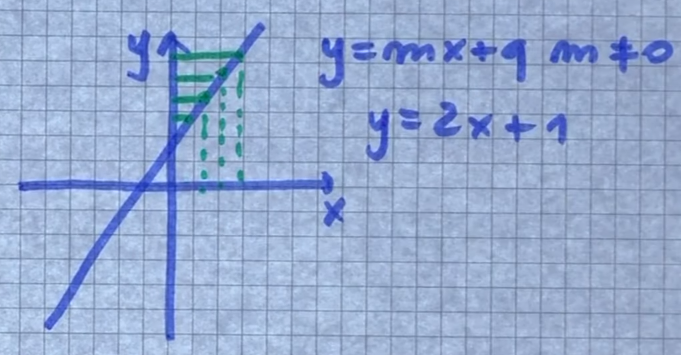
- è l’insieme delle del piano cartesiano corrisponde al dominio
- è l’insieme delle del piano cartesiano corrisponde al codominio
- ad ogni elemento di posso associare soltanto un elemento di questo posso farlo sempre
La cardinalità di un insieme è definita come il numero di elementi che appartengono all’insieme, per riuscire a contare questi elementi si cerca una corrispondenza biunivoca tra l’insieme e un insieme “campione” fatto da numeri naturali detto ovvero l’insieme dei numeri naturali interi che precedono ( es: {0, 1, 2, · · · , n − 1} ), infatti:
- Insieme finito: si dice che un insieme è finito se esiste un tale che si possa mettere in corrispondenza biunivoca con ;
- Insieme infinito: Se non esiste un numero naturale tale da costruire un insieme grande quanto , l’insieme è infinito.
Teorema: Se e sono due insiemi finiti ed esiste una funzione iniettiva , allora la cardinalità di è minore o uguale alla cardinalità di , cioè
Dimostrazione: Si considera l’immagine , cioè l’insieme di elementi di a cui viene mappato. Poiché è iniettiva, ogni elemento di corrisponde a un elemento unico di , quindi . Tuttavia, è un sottoinsieme di (cioè tutti gli elementi di appartengono a ), quindi . Da qui segue che . (Ricordiamo che essendo iniettiva la funzione non tutti gli elementi di B(codominio) hanno un immagine in A(dominio))
Proprietà delle relazioni
Sia dato un insieme U diremo che una relazione definita in è:
- Riflessiva: se risulta vero che .
- R = { (1,1), (2,2) } è riflessivo
- R = { (1,1), (2,2), (1,3) } non è riflessivo
- Simmetrica: se risulta vero che e anche
- R = {(1,2),(2,1)} è simmetrico
- R = {(1,2),(2,1),(1,3)} non è simmetrico
- Transitiva: se risulta vero che e allora ci deve essere anche una
- Esempio fatto durante l’esercitazione:
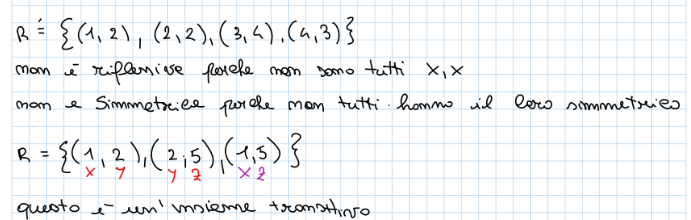
Nota
Una relazione che è sia riflessiva, simmetrica e transitiva si dice relazione di equivalenza. Più in generale una relazione di equivalenza è una relazione tra elementi di un insieme che li “raggruppa” in base a certe proprietà comuni. si indica in questo modo:
Se hai un insieme e una relazione di equivalenza su questo insieme, puoi prendere un elemento di e formare un sottoinsieme di , che contiene tutti gli elementi che sono equivalenti a . Questo sottoinsieme è chiamato classe di equivalenza di , e si indica con .
Per le classi di equivalenza vale il seguente teorema: Teorema: Due classi di equivalenza o sono disgiunte o coincidono. Dimostrazione: Siano e due classi di equivalenza e supponiamo che esse abbiano un elemento in comune: pertanto è e . Allora, per la proprietà transitiva è . Sia ora , cioè . Per la proprietà transitiva è , cioè . Quindi, . Analogamente si dimostra che . Spiegazione della dimostrazione:
- Prima parte: Supponiamo che le classi e abbiano un elemento in comune
- Se è in comune, significa che e
- Per la proprietà transitiva della relazione di equivalenza, se e , allora
- Seconda parte: Dimostriamo che ⊆
- Prendiamo un elemento qualsiasi
- Per definizione di classe di equivalenza, significa che
- Sappiamo già che (dalla prima parte)
- Per la proprietà transitiva, se e , allora
- Quindi
- Poiché questo vale per ogni , abbiamo dimostrato che
- Terza parte: Analogamente si dimostra che
- Il ragionamento è lo stesso ma invertendo x e z
- Conclusione:
- Se e , allora
- Questo dimostra che se due classi di equivalenza non sono disgiunte (cioè hanno un elemento in comune), allora devono necessariamente coincidere. In altre parole, non possono “sovrapporsi parzialmente” o non hanno elementi in comune (sono disgiunte) o sono esattamente le stesse (coincidono).
Data una relazione su un insieme , consideriamo ora la famiglia di insiemi formata da tutte le classi di equivalenza create dalla relazione su . è un sottoinsieme di [#insieme-delle-parti|pow] tale che:
- L’unione di tutte le classi di equivalenza che appartengono ad ci da
- per ogni X , Y ∈ F, X Y si ha X ∩ Y = ∅ (vedi teorema precedente) Quindi, una relazione di equivalenza individua una partizione su che viene detta Insieme Quoziente e lo denotiamo con Esempio: Immagina U come l’insieme dei numeri interi e R come la relazione “avere lo stesso resto nella divisione per 3” : = {…, -3, 0, 3, 6, …} = {…, -2, 1, 4, 7, …} = {…, -1, 2, 5, 8, …} Queste tre classi formano una partizione di ovvero , che si può anche chiamare Insieme quoziente di U. Quindi capiamo subito che
Individuato l’insieme quoziente (che denotiamo con ), l’applicazione , ovvero un’applicazione che associa ogni alla sua classe di equivalenza. Questa è un’applicazione surgettiva perché ogni classe di equivalenza è effettivamente “raggiunta” da almeno un elemento di . Questa applicazione viene anche chiamata applicazione canonica sul quoziente.
Nota
Differenza tra applicazione e funzione Nel contesto specifico dell’applicazione canonica sul quoziente, si parla di applicazione perché si vuole mettere in evidenza il fatto che stiamo “applicando” una trasformazione sugli elementi dell’insieme . In particolare, stiamo usando una regola (la relazione di equivalenza) per trasformare ogni elemento x di nella sua classe di equivalenza .
Di seguito delle definizioni:
-
Si dice che una relazione binaria si antisimmetrica se:
- si ha che: . il sussistere di entrambe le relazioni e è possibile solo quando e coincidono.
-
Si dice preordinamento una relazione binaria assegnata in un insieme che goda della proprietà riflessiva e transitiva
-
Si dice ordinata una relazione binaria assegnata in un insieme che goda della proprietà riflessiva, transitiva e antisimmetrica
Un insieme su cui è definita un relazione di pre-ordine si dice pre-ordinato. Un insieme su cui è definita un relazione d’ordine si dice ordinato.
Dato un pre-ordinamento oppure un ordinamento (rappresentato dal simbolo ≤) in un insieme U, si pone
- ovvero x è minore di y, se x è minore/uguale a y però con x diverso da y
Un ordinamento definito in un insieme si dice totale o lineare se per ogni coppia di elementi di si ha oppure . Altrimenti si dirà parziale.
Massimi e minimi
- Un elemento M di un insieme ordinato U si dice massimo se per ogni si ha
- Si dice invece massimale se non vi è alcun elemento di U che lo supera.
- Un elemento m di un insieme ordinato U si dice minimo se per ogni si ha .
- Si dice invece minimale se non vi è alcun elemento di U ad esso inferiore
Il massimo (minimo) in un insieme è unico, il massimale (minimale) invece si può riscontrare più volte, questo accade perché potrebbe succedere che due elementi non siano confrontabili tra loro e quindi sono dei massimali.
Sia quindi dal momento che A è finito, possiamo dire che A ⊆ per qualche intero . con intendiamo un insieme fatto cosi {0,1,2, … , m-1}. Esistono diversi modi per rappresentare A ⊆
- Rappresentazione binaria: la struttura dati più semplice che potremmo usare è un’array fatto da valori binari
- = 1 se
- = 0 se
- Rappresentazione estesa: si può anche usare un’array di interi Y con |A| = n elementi tale che se A = {, , … , } allora per ogni =
Se utilizziamo la rappresentazione binaria, verificare che un elemento i ∈ A prende tempo costante. Se utilizziamo la rappresentazione estesa, invece, ed A non è ordinato, dobbiamo scorrere tutta l’array e quindi tempo lineare. Se l’array è ordinata invece si può fare in tempo logaritmico. D’altro canto, se utilizziamo la rappresentazione binaria, per l’insieme A = {10, 3, 99} serve un’array di dimensione 100, mentre, se utilizziamo la rappresentazione estesa, serve un’array di dimensione 3.
Se prendiamo ovvero {0, 1, 2, … , n − 1} gli elementi di sono i numeri binari esprimibili con bits. Quindi .
Siano un insieme finito, , e sia una famiglia di sottoinsiemi di U tutti diversi dall’insieme vuoto. Diciamo che è un hitting set () per se e solo se per ogni si ha ∅
Sia = {a, b, c, d, e} e sia A = {{a, b, c, }, {a, d, e}, {b, c, d, }, {c, d, e}}. L’insieme {a, b, c} è un per mentre {b, c} o {d, e} non lo sono.
- {a, b, c} è un hitting set perché:
- Contiene ‘a’, che è presente anche in {a, d, e}.
- Contiene ‘b’, che è presente anche in {b, c, d}.
- Contiene ‘c’, che è presente anche in {c, d, e}.
- In altre parole, questa scatola più piccola “colpisce” (interseca) tutte le altre scatole.
- {b, c} e {d, e} non sono hitting set perché:
- {b, c} non contiene alcun elemento presente in {a, d, e}.
- {d, e} non contiene alcun elemento presente in {a, b, c}.
Possono esistere diversi hitting set dentro un’insieme, si definisce hitting set minimo l’hitting set con meno elementi, nell’esempio sopra descritto un hitting set minimo sarebbe {a, c} visto che contiene almeno un elemento di ogni insieme contenuto in
Il problema di trovare un minimo per una famiglia di insiemi è facilmente risolvibile: basta provare per tutti i sottoinsiemi di . Questo però vorrebbe dire che il numero di operazioni da fare è esponenziale visto che i sottoinsiemi non vuoti di sono esattamente
- Per |U| = 100 il numero totale di operazioni sarebbe dell’ordine di 1, 26 · Esiste un modo migliore? non si sa! L’unico modo per cercare di risolvere questo tipo di problematiche è usare degli algoritmi detti greedy ciò vuol dire nello specifico, che potremmo prendere l’elemento di U che appartiene al maggior numero di elementi di Poi, per tutti gli elementi di a cui non appartiene, scegliamo l’elemento che appartiene alla maggior parte di essi, e così via.