Come creare tutte le combinazioni tra le variabili senza confondersi
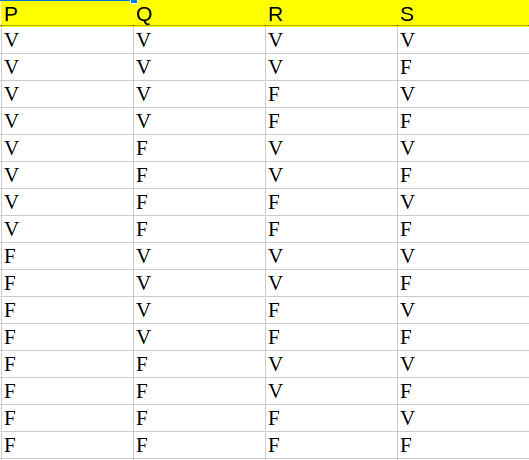 Numero variabili da rappresentare: 4 (P,Q,R,S)
Numero casi possibili: nCasi = =
Per la prima variabile:
Numero variabili da rappresentare: 4 (P,Q,R,S)
Numero casi possibili: nCasi = =
Per la prima variabile:
- scrivi 8 volte V e 8 volte F Per la seconda variabile scrivi:
- 4 volte V - 4 volte F - 4 volte V - 4 volte F Per la terza variabile scrivi:
- 2 volte V - 2 volte F - 2volte V - 2 volte F - 2 volte V - 2 volte F - 2 volte V - 2 volte F Per la quarta variabile scrivi:
- VERO - FALSO - VERO - FALSO … fino a quando non arrivi a nCasi
Se hai una tabella con 6 variabili sono 64 casi e la prima variabile sarà 32 volte vero e 32 volte falso, ogni volta che cambi variabile dividi per 2 i casi veri e quelli falsi
Come distribuire le congiunzioni sulle disgiunzioni e viceversa
Formula iniziale:
- Riscrivo la variabile e l’operatore logico che sono fuori dalla parentesi e tra le 2 (2 sono il numero di variabili dentro la parentesi) parantesi che avrò metto l’operatore logico che c’è dentro la parentesi.
- () ∨ ()
- Metto al posto dei puntini le variabili che ho dentro la parentesi, non è importante l’ordine
- () ∨ ()
Formula finale: () ∨ ()
Come calcolare la chiusura di una famiglia rispetto ad unione/intersezione
= {1, 2, … , m} = ??? famiglia più piccola che contiene ed è chiusa rispetto all’unione
- Costruiamo la famiglia mettendoci tutti gli elementi di .
- Per ogni i (partendo da 2) sino a m calcoliamo utilizzando tutte le coppie di elementi , con e e mettendo in .
- Poniamo infine
Come trasformare una qualsiasi formula in CNF e DNF
- Elimina le coimplicazioni p ⇔ q dalla formula sostituendole con (p ⇒ q) ∧ (q ⇒ p)
- Elimina le implicazioni p ⇒ q dalla formula sostituendole con ¬p ∨ q
- Sposta le negazioni a ridosso delle variabili proposizionali ed elimina le doppie negazioni.
- Di Bella move:
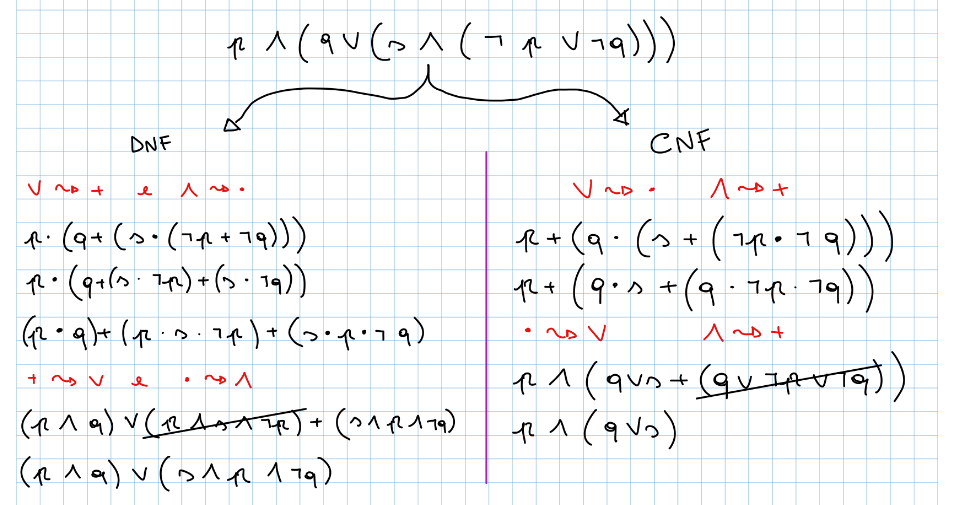 Questo passaggio consiste nel trasformare il tutto in moltiplicazione e somme per rendere tutto più intuitivo.
Questo passaggio consiste nel trasformare il tutto in moltiplicazione e somme per rendere tutto più intuitivo.
Differenza tra applicazione e funzione
In matematica, i termini “applicazione” e “funzione” sono praticamente sinonimi, ma ci sono alcune sottili differenze di uso e di contesto che spiegano perché in certi casi si preferisce usare uno rispetto all’altro.
-
Funzione: La parola “funzione” è il termine più generico e formale per descrivere una corrispondenza tra due insiemi, dove ad ogni elemento del primo insieme (detto dominio) corrisponde uno e un solo elemento del secondo insieme (detto codominio). Quindi, una funzione è una regola che associa elementi del dominio al codominio. Formalmente, una funzione è una relazione che associa ad ogni elemento di un unico elemento di .
-
Applicazione: Il termine “applicazione” è usato in contesti più specifici o pratici. Spesso viene utilizzato quando si vuole enfatizzare il processo o l’atto di associare un elemento del dominio al suo corrispondente nel codominio, piuttosto che la funzione come oggetto matematico in astratto. “Applicazione” sottolinea l’idea di “applicare” una regola o un’operazione a un elemento per ottenere un risultato.