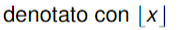02_Parte2

Questo file è la rielaborazione delle slide 02_Parte2.pdf

Numeri interi

Sull’insieme N sono definite 2 operazione:

• Somma: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n+m\in N$
• Prodotto: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n\ast m\in N$ Sull’insieme Z sono definite 3 operazioni:
• Somma e prodotto come definite per N
• Differenza: operazione che ad ogni coppia di numeri $(n,m)$ associa il numero $n-m$ ∈ Z
• In Z definiamo anche il valore assoluto in questo modo $|n|=\{\begin{array}{ll}n& \text{se }n\ge 0\\ -n& \text{se }n<0\end{array}$ Giuseppe Peano dà una definizione dell’insieme dei numeri naturali in questo modo:
• Esiste un numero naturale 0
• Ogni numero naturale $a$ ha un numero naturale successore denotato come $S(a)$
• Non esiste un numero naturale il cui successore è 0
• Numeri naturali distinti hanno successori distinti

Introducendo la funzione successore (S(a)) è possibile definire una relazione di ordinamento sui numeri naturali, questo viene chiamato assioma del buon ordinamento infatti in un generico insieme S esiste un elemento minimo ovvero esiste un elemento s ∈ S tale che s ≤ t per ogni t ∈ S.

Ricordiamo:

• le proprietà fondamentali della somma sono Commutatività, Associatività e Elemento neutro
• le proprietà fondamentali del prodotto sono Commutatività, Associatività, Distributività, Elemento neutro e Elemento zero
• inoltre il calcolo avviene rispettando le priorità degli operatori

Peano introduce anche un altro concetto detto “Principio di induzione” che dice

• Se una proprietà $P$ è posseduta dal numero $0$ e la proprietà $P$ è posseduta anche dal successore di ogni numero naturale che possiede la proprietà P, allora la proprietà P è posseduta da tutti i numeri naturali.

Esempio principio di induzione.pdf

Sia x un numero reale, definiamo i 2 seguenti valori:

• “Floor”: il più grande numero intero minore o uguale ad x
  • 
• “Ceiling”: il più piccolo numero intero maggiore o uguale ad x
  • Esempi:

---

Divisione tra interi

Dati due interi $a,b\in Z$, chiamati rispettivamente dividendo e divisore, esistono unici due interi relativi $q,r$, denominati rispettivamente quoziente e resto, tali che $a=q\cdot b+r$ con $0\le r<|b|$.

Legenda

a = dividendo b = divisore q = quoziente r = resto

In questo tipo di divisione noi abbiamo 4 casi:

• Nel primo caso assumiamo che il dividendo a ed il divisore b siano entrambi non negativi
  • É sempre possibile trovare un unico quoziente $q$ e un unico resto $r$ tali che:
    • $a=qb+r$
    • $q=\frac{a}{b}$ come risultato prendo solo la parte intera
    • $r=a+qb$
    • $0<=r<b$
  • $a=1$, $b=10$: $q=\frac{1}{10}=0$ e $r=\frac{1}{10}\times 10=1$ quindi ==1 mod 10 = 1==
• Nel secondo caso assumiamo che il dividendo a sia negativo ma il divisore b positivo
  • Assumiamo allora che $a<0$ mentre $b>0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(-q^{\prime })b+(-r^{\prime })$
    • $q=-q^{\prime }-1$
    • $r=b-r^{\prime }$
  • $a=-1$, $b=10$: per $a=1$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per a = -1 abbiamo $q^{\prime }=-1$ e $r^{\prime }=10-1=9$ quindi ==-1 mod 10 = 9==
• Nel terzo caso assumiamo che il dividendo a sia positivo e il divisore b negativo
  • Assumiamo allora che $a>0$ e $b<0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(-q^{\prime })b+(-r^{\prime })$
    • $q=-q^{\prime }$
    • $r=r^{\prime }$
  • $a=1$, $b=-10$: per $b=10$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per b = -10 abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ quindi ==1 mod -10 = 1==
• Nel quarto caso assumiamo che il dividendo a ed il divisore b siano entrambi negativi
  • Adesso assumiamo che $a<0$ e $b<0$, chiameremo $q^{\prime }$ e $r^{\prime }$ i risultati del primo caso da cui otteniamo:
    • $a=(q^{\prime }+1)b-b-r^{\prime }$
    • $q=-q^{\prime }+1$
    • $r=-b-r^{\prime }$
  • $a=-1$, $b=-10$: per $a=1$ e $b=10$ abbiamo $q^{\prime }=0$ e $r^{\prime }=1$ e quindi per $a=-1$ e $b=-10$ abbiamo $q^{\prime }=1$ e $r^{\prime }=10-1=9$ quindi ==-1 mod -10 = 9==

Riepilogando, dati due interi a, b ∈ Z con $\ne$ 0, per trovare quoziente e resto r positivo della divisione a b agiamo così:

• Troviamo il $q\prime$= $\frac{|a|}{|b|}$ ovvero il massimo intero $q\prime$ tale che $|a|-q|b|\ge 0$ e fissiamo $r\prime =|a|-q\prime |b|$. Se $a,b\ge 0$ poniamo $q=q\prime$ e $r=r\prime$.
• Se $a<0$ e $b>0$ poniamo $q=-q\prime -1$ e $r=b-r\prime$.
• Se $a>0$ e $b<0$ poniamo $q=-q\prime$ e $r=r\prime$.
• Se $a<0$ e $b<0$ poniamo $q=q\prime +1$ e $r=-b-r\prime$.

---

Definizione di divisibilità

Dati 2 interi relativi $n,m\in Z$ si dice che m è un divisore di n se esiste un intero relativo $k\in Z$ tale che n = $k\ast m.$ In altre parole m è un divisore di n se $n$ mod $m$ è uguale a 0, in tal caso useremo la notazione $m|n$. Se m non è un divisore di n quindi $n$ mod $m$ è diverso da 0 usiamo la notazione $m\nmid n$

• un numero $m|2$ si dice pari
• un numero $m\nmid 2$ si dice dispari visto che il resto della sua divisione per 2 è uguale ad 1 esiste un intero k tale che
• $n=2k+1$

---

Dimostrazione per induzione che la somma dei primi n numeri dispari è $n^2$

• Caso base: n = 1 e la somma in questo caso è proprio $1=1^2$
• Caso induttivo: Assumendo che la somma dei primi n-1 numeri dispari è uguale a $(n-1{)}^2$ e un generico numero dispari è definito con: $n=2k+1$, quindi se aggiungiamo a $(n-1{)}^2$ il numero dispari successivo quindi $2(n-1)+1$ otteniamo:
• $(n-1{)}^2+2(n-1)+1=n^2-2n+1+2n-2+1=n^2$ Esempio: $n=5$ $n^2=5^2=25$ $(5-1{)}^2+2(n-1)+1=16+9=25$

---

Proprietà della divisibilità

• Somma: Se $a|b$ e $a|c$ allora $a|(b+c)$
• Prodotto: Se $a|b$ allora $a|bc$.
• Transitività: Se $a|b$ e $b|c$ allora $a|c$
• Quadrato: Se $a|b$ allora $a|b^2$
  • Dimostrazione: Dato che $a|b$ esiste $x$ tale che $b=ax$, quindi $bc=axc$ questi dimostra che $a|b\ast b$
• Combinazione lineare: Se $a|b$ e $a|c$ allora $a|(hb+kc)$ per ogni $h,k\in Z$
  • Dimostrazione: Se $a|b$ allora $a|hb$, se $a|c$ allora $a|kc$ ovviamente valgono per ogni $h,k\in Z$ e quindi è vero che a | (hb + kc)
• Proprietà del numero 0: Ogni $a\in Z$ è divisore di 0
  • Dimostrazione: $a\in Z$ abbiamo che $a\ast 0=0$ quindi $a|0$
• Antisimmetrica: Siano $a,b\in Z$ se $a|b$ e $b|a$ allora $|a|=|b|$ ossia $a=\pm b$
  • Dalle ipotesi abbiamo che $b=ax$ e $a=by$. Quindi $a=axy$, raccogliendo a arriviamo ad $a(xy-1)$ questo implica che $a$ sia $0$ oppure che $xy=1$ da questo capiamo che:
    • Se $a=0$ allora anche b = 0 (perché b = 0x)
    • Se $xy=1$ allora a o b sono uguali a $\pm 1$
• Divisori banali: Siano a $\in$ Z allora $\pm a|a$ e $\pm 1|a$
  • Avendo che $a=a\cdot 1$ oppure che $a=(-a)\cdot (-1)$ possiamo affermare che $\pm a|a$
    • Seguendo la definizione capiamo che $a=b\cdot k$ in questo caso $b=\pm a$ il k che soddisfa le nostre equazioni è k = 1
  • Avendo che $a=1\ast a$ possiamo dire che 1 è sempre un divisore di $a$

---

Minimo Comune Multiplo

Dati $a,b\in Z$ si chiama minimo comune multiplo fra a e b un terzo intero positivo m che è il più piccolo multiplo sia di $a$ che di $b$, quindi possiamo affermare che $a|m$ e $b|m$

Massimo Comune Divisore

Dati $a,b\in Z$ si chiama Massimo Comune Divisore un terzo intero $d\in Z$ tale che $d|a$ e $d|b$ cioè $d$ è il più grande divisore comune tra $a$ e $b$.

Il metodo migliore per calcolare il massimo comune divisore è l’algoritmo di euclide, che si basa su questa osservazione siano $a,b\in N$ e sia $b<=a$ (di seguito la dimostrazione per induzione):

• Caso base se b = 0 allora il $MCD(a,b)=a$
• Passo induttivo: visto che $a=qb+r$ con $0<r<b$ allora $MCD(a,b)$ = $MCD(b,r)$ Da questo notiamo che se $b|a$ allora $a=qb$ ($q$ sarebbe $\frac{a}{b}$) perché abbiamo resto 0 quindi la formula diventa $MCD(a,b)$ = $MCD(b,0)$ = $b$. In conclusione se $b|a$ otteniamo che $MCD(a,b)=b$

Dimostriamo che $MCD(a,b)$ = $MCD(b,r)$

• Se $d$ è un divisore di $a$ e $b$ allora esistono $h$ e $k$ tali che $d$ sia un divisore di $r$ (la formula base per calcolare $r$ è $r=a-qb$ )
  • $a=hd$
  • $b=kd$
  • $r=hd-qkd=d(h-qk)$ (essendo che r può essere scritto come $d$ * un’intero allora è vero che $d$ è un divisore di $r$ Definizione di divisibilità)
• Se invece $d$ è un divisore di $b$ e di $r$ allora esistono $h$ e $k$ tali che $a$ è un divisore di $m$ (ricordiamo che la formula base per calcolare $a$ è $a=qb+r$):
  • $b=kd$
  • $r=hd$
  • $a=qkd+hd$ = $d(qk+h)$ (essendo che $a$ può essere scritto come d * un intero allora è vero che è un divisore di b Definizione di divisibilità) Esempio $x_1=330$ e $x_2=156$ $x_3=330\mathrm{mod}156=18$ $x_4=156\mathrm{mod}18=12$ $x_5=18\mathrm{mod}12=6$ $x_6=12\mathrm{mod}6=0$ Quindi $MCD(330,156)=6$. Da questo capiamo che il minimo comune divisore tra 2 numeri può essere calcolato trovando ripetutamente il modulo tra b ed il resto

Siano $a,b\in N$ allora esistono $h,k\in Z$ tali che $MDC(a,b)=a\ast h+b\ast k$ Questo vuol dire che il MCD tra due numeri si può scrivere come una loro combinazione lineare Esempio partendo dall’esempio precedente e andando a ritroso: $6=18-12$ $=18-(156-8\ast 18)$ $=-156+9\ast 18$ $=-156+9(330-2\ast 156)$ $=-19\ast 156+9\ast 330$

---

Numeri primi e coprimi

Si definisce numero primo un intero che ha come divisori quelli banali ovvero 1 e se stesso. Due numeri $a,b\in Z$ si dicono coprimi se $MCD(a,b)=1$ quindi esistono $h,k\in Z$ tali che (a · h + b · k) = 1

Come conseguenza del seguente teorema abbiamo le seguenti proprietà

1. Due numeri interi consecutivi sono coprimi
2. Siano $a,b,c\in Z$ tali che $c|a\ast b$ con $c$ ed $a$ coprimi allora $c|b$
   1. Abbiamo che $9|3\ast 6$ però notiamo che $9\nmid 3$ infatti $c$ ed $a$ non sono coprimi
3. Siano $a,b,c\in Z$ tali che $a|c$ e $b|c$ se $a$ e $b$ sono coprimi allora $a\ast b|c$
   1. Abbiamo che $4|12$ e $6|12$ ma $24\nmid 12$ infatti $a$ e $b$ non sono coprimi

---

Fattorizzazione degli interi

Ogni intero n > 1 si può esprimere come prodotto di numeri primi positivi ed in modo unico Dimostrazione: la dimostrazione di questo teorema deve essere fatta in 2 passi distinti

1. Prima dimostriamo che preso un qualunque n > 1 esiste una fattorizzazione di n;
   • Se per assurdo esistessero interi > 1 che non sono prodotto di numeri primi positivi potremmo costruire l’insieme $S=n:n\in N$ con n che è un numero non prodotto di numeri primi. Per l’assioma del buon ordinamento, dentro questo insieme abbiamo un minimo che chiameremo $s$, $s$ non è primo (perché senno sarebbe un prodotto di numeri primi positivi) quindi vuol dire che ha almeno un divisore non banale positivo chiamato $d$, avendo un divisore vuol dire che esiste un intero positivo che $c$ che moltiplicato per $d$ ci da $s$, $c$ e $d$ sono prodotti di primi positivi, e quindi anche $s$ lo è
2. successivamente dimostriamo che quella fattorizzazione è unica
   • Se $n=p_1\cdot p_2\cdots p_r=q_1\cdot q_2\cdots q_s$ ovvero $n$ è la somma dei primi $r$ o $s$ numeri interi ($p_i$ e $q_i$ sono gli i-esimi numeri primi ). La dimostrazione che va fatta è che $r$ = $s$, di seguito la dimostrazione per induzione.
     • Caso base: $r=1$ Se $n=p_1$ allora $n$ è primo, da $p_1=q_1\cdot q_2\cdots q_s$ otteniamo che $s=1$ e $q_1=p_1$
     • Caso induttivo: supponendo che sia vera questa tesi per r, dimostriamola per r+1, quindi: $n=p_1\cdot p_2\cdots p_{r+1}=q_1\cdot q_2\cdots q_s$ , dal caso base sappiamo che $q_1$ è divisore di $p_1$ e che quindi dividendo membro a membro per $p_1$ otteniamo $p_2\cdots p_r\cdot p_{r+1}=q_2\cdots q_s$ da questo capiamo che $r=s-1$ e quindi che $s=r+1$ quindi i fattori coincidono a meno dell’ordine e quindi che sono uguali.

---

Teorema di euclide

I numeri primi sono infiniti. Dimostrazione:

1. Ipotesi di assurdo: Supponiamo che ci sia un numero finito di numeri primi. Se così fosse, potremmo elencarli tutti. Chiamiamo questi numeri primi $p_1,p_2,\dots ,p_n$, dove $p_1=2$, $p_2=3$, e così via fino a $p_n$, che rappresenterebbe l’ultimo numero primo.
2. Costruzione di un nuovo numero: Consideriamo il numero $h$ definito come il prodotto di tutti questi numeri primi più uno: $h=p_1\cdot p_2\cdots p_n+1$
3. Proprietà di $h$:
   • Per costruzione, $h$ è maggiore di tutti i numeri primi $p_1,p_2,\dots ,p_n$.
   • Inoltre, $h$ non è divisibile da nessuno dei numeri primi $p_1,p_2,\dots ,p_n$. Infatti, se dividiamo $h$ per uno qualsiasi di questi numeri primi $p_i$, otteniamo un resto di 1. In altre parole, $h\mathrm{mod}{p}_i=1$, per ogni $i=1,2,\dots ,n$.
4. Contraddizione:
   • A questo punto, possiamo concludere che $h$ o è primo oppure è divisibile da un numero primo non presente nella lista $p_1,p_2,\dots ,p_n$.
   • Se $h$ è primo, allora abbiamo trovato un nuovo numero primo che non era incluso nella lista originale, il che contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ fossero tutti i numeri primi.
   • Se $h$ non è primo, allora deve avere un divisore primo che non è nessuno dei $p_1,p_2,\dots ,p_n$, il che ancora una volta contraddice l’ipotesi che $p_1,p_2,\dots ,p_n$ siano tutti i numeri primi.

I numeri primi non solo sono infiniti, ma sono anche distribuiti in maniera tale da essere molto frequenti Sia $n\in N$ sia $\pi (n)$ il numero di numeri primi minori o uguali ad n. Allora ${\lim }_{n\to \infty }\frac{\pi (n)}{\frac{n}{\ln n}}=1$ da questo estraiamo la seguente formula: $\frac{n}{\ln n}$ che ci va ad indicare il numero di numeri primi < di n

• per n = 100 stimati $\frac{100}{\ln 100}\approx 22$
• per n = 1000 stimati $\frac{1000}{\ln 1000}\approx 145$

---

Come verificare se un numero n è primo?

Verificando che non abbia divisore diversi da quelli banali. Ciò può essere fatto in maniera più efficiente se durante la verifica consideriamo i numeri compresi tra 2 e $\sqrt{n}$

---

Crivello di Eratostene

Se abbiamo la necessità di calcolare tutti i numeri primi minori o uguali ad un numero n, possiamo usare il crivello di Eratostene, questi sono i passaggi da seguire:

1. Scriviamo in sequenza tutti i numeri naturali compresi tra 2 e n.
2. Partiamo dal numero 2 e cancelliamo tutti i suoi multipli
3. Ad ogni passo prendiamo il primo numero tra i numeri che seguono e cancelliamo i suoi multipli
4. Quando abbiamo cancellato tutti i multipli del numero più grande che sia minore o uguale $a\sqrt{n}$ ci fermiamo. Esempio

---

Radice numerica

Dato un numero $n$ la sua radice numerica di $n$, la denotiamo con $\rho (n)$ ed è la somma delle sue cifre reiterata sono ad ottenere una sola cifra

• $198:1+9+8=18\to 1+8=9$ e quindi $\rho (198)=9$.

Criteri di divisibilità

Esistono delle regole molto semplici per verificare la divisibilità di un numero $a$ per un numero $b$

• Divisibilità per 2: un numero è divisibile per $2$ se è pari
  • 4 è divisibile per 2
• Divisibilità per 3: un numero è divisibile per $3$ se la somma delle sue cifre è un numero divisibile per $3$
  • 81 = 8 + 1 = 9 è divisibile per 3
• Divisibilità per 5: un numero è divisibile per $5$ se l”ultima cifra è $0$ o $5$
  • 105 è divisibile per 5
• Divisibilità per 7: un numero è divisibile per $7$ se $q-2r$ è divisibile per $7$
  • $q=$ quoziente della divisione con 10
  • $r=$ resto della divisione con 10
  • $161:16-2\ast 1=14$ che è divisibile per 7
• Divisibilità per 11: un numero è divisibile per $11$ se $a-b$ è divisibile per 11
  • $a=$ somma dei numeri nelle posizioni dispari
  • $b=$ somma dei numeri nelle posizioni pari
    • 2805 quindi con
      • $a=2+0$
      • $b=8+5$
      • $a-b=-11$ che è divisibile per 11
• Divisibilità per 9: un numero $n$ è divisibile per $9$ se la sua radice numerica è divisibile per 9, oppure se $n-\rho (n)$ è divisibile per 9.
  • $198:1+9+8=18\to 1+8=9$ e quindi 198 è divisibile per 9
• Divisibilità per altri numeri primi:
  • $13$ divide n se $q+4r$ è divisibile per $13$
  • $17$ divide n se $q-5r$ è divisibile per $17$
  • $19$ divide n se $q+2r$ è divisibile per $19$
  • $23$ divide n se $q+7r$ è divisibile per $23$
    • $q=$ quoziente della divisione con $10$
    • $r=$ resto della divisione con $10$
  • Esempi qui

---

Dimostrazione per assurdo che $\sqrt{2}$ non è razionale

Assumendo che esistano 2 numeri naturali $a$ e $b$ tale che $\sqrt{2}=\frac{a}{b}$, assumendo anche che sia ridotta ai minimi termini almeno uno dei 2 è dispari. Elevando al quadrato otteniamo $a^2=2b^2$ essendo $a^2$ il doppio di un altro numero sarà per forza pari, detto ciò anche $a$ è pari è quindi esiste un numero $k$ tale che $a=2k$ da questo avremo allora:

• $2b^2=a^2=4k^2$ e quindi che anche $b$ è pari visto che $b^2=2k^2$ questa affermazione contraddice la nostra ipotesi inziale

---

Aritmetica modulare

L’aritmetica modulare riguarda il calcolo sui resti delle divisioni tra interi rispetto ad un divisore fissato. Ricordiamo la Divisione tra interi e diciamo che con la dicitura n mod m, indichiamo con $n$ la base e con $m$ il modulo. Fissando un intero relativo $m$, possiamo definire la congruenza modulo $m$ in questo modo:

• un intero $a\in Z$ è in relazione con $b\in Z$ se $m|(a-b)$ e quindi che $a-b$ è un multiplo di $m$. In modo equivalente potemmo dire che $a$ è in relazione con $b$ se $a$ mod $b$ = $b$ mod $m$
• Se si verificano queste condizioni, la relazione tra a e b si scrive così:
  • $a\equiv b(\mathrm{mod}m)$
    • 12 ≡ 9(mod 3) : $12$ mod $3$ = $9$ mod $3$ = $0$ entrambi per il primo caso del teorema della divisione
• Se non si verificano queste condizioni, la relazione tra a e b si scrive così:
  • $a\not\equiv b(\mathrm{mod}m)$
    • $7\not\equiv 1(\mathrm{mod}4)$ infatti $7$ mod $4$ = $3$ mentre $1$ mod $4$ = $1$

Da tutto ciò notiamo che per ogni $a\in Z$ ed ogni $m\in N$ abbiamo che:

• $a\equiv a\mathrm{mod}m(\mathrm{mod}m)$
  • $5\equiv 5\mathrm{mod}10(\mathrm{mod}10)$ se risolvi $5\mathrm{mod}10$ si capisce in modo intuitivo la proprietà

La relazione di congruenza è una relazione di equivalenza e ciò implica che abbiamo un infinità di relazioni di equivalenza, di seguito la dimostrazione:

• Riflessiva: per ogni $a\in Z$ è vero che $a\equiv a\mathrm{mod}m$ perché essendo che $0=a-a$ e $0$ è divisibile per qualsiasi numero anche $a$ è divisibile per qualsiasi numero (Ricordiamo che la congruenza è vera se $m|(a-b)$ (questa formula è importante per tutte le spiegazioni successive) dove in questo caso $b=a$)
• Simmetrica: Se $a\equiv b(\mathrm{mod}m)$ allora $a-b=km$ per qualche $k\in Z$ e quindi, moltiplicando per $-1$ otteniamo $-a+b=(-k)m$ ossia $b\equiv a(\mathrm{mod}m)$
• Transitiva: Se $a\equiv b(\mathrm{mod}m)$ e b ≡ $c(\mathrm{mod}m)$ abbiamo che esistono $h,k\in Z$ tali che $a-b$ = $hm$ e $b-c=km$. Sommando membro a membro le ultime due uguaglianze otteniamo: $a-c=(h+k)m$ e quindi $a\equiv c(\mathrm{mod}m)$.

Classi di equivalenza definite dalla congruenza

• Congruenza modulo 0: $a\equiv b(\mathrm{mod}0)$ se e solo se $a-b=k\cdot 0$ ovvero $a-b=0$ quindi se $a=b$
  • Tutte le classi di equivalenza create dalla congruenza modulo 0 sono delle classi contenenti un solo elemento (ovvero quello preso in esame)
    • In questo caso la classe di equivalenza di $a$ è {$a$}
• Congruenza modulo 1: $a\equiv b(\mathrm{mod}1)$ se e solo se $a-b=k\cdot 1$ ovvero $a-b$ è multiplo di 1
  • Essendo che ogni numero è multiplo di 1 la classe di equivalenza creata dalla congruenza modulo 1 contiene tutti gli interi $\in Z$
• Congruenza modulo 2: $a\equiv b(\mathrm{mod}2)$ se e solo se $a-b=k\cdot 2$ ovvero $a-b$ è un numero pari
  • Se $a$ è pari abbiamo che $a=2\ast h$ e quindi che $b=2h-k\ast 2=2(h-k)$ e quindi anche $b$ è pari
  • Se $a$ è dispari abbiamo che $a=2\ast h+1$ e quindi che $b=2h+1-k\ast 2=2(h-k)+1$ e quindi anche $b$ è dispari
  • Le classi di equivalenza create sono 2 una con tutti i numeri dispari e una con tutti i numeri pari Dato un intero m >= 0 indicheremo con $[a{]}_m$ la classe di rappresentata dall’intero $a$ nella relazione di congruenza modulo $m$ ovvero:
• $[a{]}_m=\{b\in \mathbb{Z}:a\equiv b(\mathrm{mod}m)\}$

Teorema Fissato un intero m > 1 le sue classi di equivalenza sono: $[0{]}_m,[1{]}_m,[2{]}_m,\dots ,[m-1{]}_m.$ Dimostrazione Sia $a\in Z$ e sia $r$ il resto della divisione intera di $a$ per $m$, ovvero, applicando l’algoritmo di divisione

• $a=qm+r$ con $0\le r<m$. Dal momento che $a-r=qm$ abbiamo che $a\equiv r(modm)$. Quindi, dal momento che $r$ può assumere solo i valori che vanno da $0$ a $m-1$ le classi di equivalenza sono solo quelle dell’enunciato del teorema.

Dimostrazione che le classi sono distinte Ragioniamo per assurdo e supponiamo che esistano $x,y\in Z$, $x\ne y$ e $0\le x$, $y<m-1$ tali che $[x{]}_m$ = $[y{]}_m$ . Senza perdita di generalità supponiamo che $x>y$. Dall’ipotesi possiamo scrivere $x-y=km$ cioè $x-y$ è un multiplo di $m$. Da $0\le x,y<m-1$ e $x>y$ segue che $0<x-y<m-1$, che è una contraddizione visto che non esistono multipli di m in tra $0$ e $m-1$.

Sia $m=5$ (congruenza modulo $5$). Le classi resto modulo $5$ sono $[0{]}_5,[1{]}_5,[2{]}_5,[3{]}_5,[4{]}_5.$

Nota

Esempio:

• $[2{]}_5$ Sono tutti quei numeri che divisi per 5 ci danno resto 2
• $[5{]}_{1}0$ Sono tutti quei numeri che divisi per 10 ci danno resto 5

Dato a ∈ Z come facciamo a stabilire in quale classe resto sta?

• La risposta ci viene fornita dal teorema appena dimostrato: $[a{]}_m$ = $[r{]}_m$ dove r è il resto della divisione di a per m.
• Quindi se m = 5 e a = 22 allora eseguendo la divisione abbiamo 22 : 5 = 4 con resto di 2, ottenendo che $[22{]}_5$ = $[2{]}_5$.
• Ricordiamo che la notazione $[a{]}_m$ indica la classe di equivalenza modulo $n$, cioè l’insieme di tutti i numeri interi che, divisi per $n$, lasciano lo stesso resto di $a$. Nel nostro caso:
  • $[22{]}_5$: Questa classe contiene tutti i numeri che, divisi per 5, lasciano resto 2. Alcuni esempi sono: 2, 7, 12, 17, 22, …
  • $[2{]}_5$​: Questa classe contiene tutti i numeri che, divisi per 5, lasciano resto 2. Alcuni esempi sono: 2, 7, 12, 17, …
  • le due classi contengono esattamente gli stessi elementi
• In altre parole potremmo dire che $22\equiv 2(\mathrm{mod}5)$

Notiamo che in classe $[0{]}_5$ ci sono tutti i multipli di 5 ed in generale in $[0{]}_m$ ci sono tutti i multipli di m.

---

Invarianza rispetto a somma e prodotto

Dato $m\in N$ e dati $a,b\in Z$ tali che $a\equiv b(\mathrm{mod}m)$ allora prendendo $c,d\in Z$ tali che $c\equiv d(\mathrm{mod}m)$ abbiamo che:

• $a+c\equiv b+d(\mathrm{mod}m)$
• $a\ast c\equiv b\ast d(\mathrm{mod}m)$

Dimostrazione: Ipotizziamo che per ipotesi esistono $k_1$,$k_2$ tale che $a-b=k_{1}m$ e $c-d=k_{2}m$, da questo possiamo dimostrare che:

1. $(a+c)-(b+d)=(a-b)+(c-d)=(k_1$ + $k_2$)m (da questo capiamo che qualsiasi sia l’ordine delle lettere avremo sempre dei multipli di m)
2. Abbiamo $a=b+k_{1}m$ e $c=d+k_{2}m$ quindi $ac-bd=(b+k_{1}m)(d+k_{2}m)-bd=b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2=(b{k}_2+d{k}_1+k_1{k}_{2}m)m$
   • Come si arriva a questa conclusione?
     1. Sfruttiamo le ipotesi: Ricordiamo che per ipotesi abbiamo:
        • $a\equiv b(\mathrm{mod}m),$ quindi $a=b+k_{1}m$
        • $c\equiv d(\mathrm{mod}m),$ quindi $c=d+k_{2}m$
     2. Sostituiamo nella moltiplicazione: Moltiplichiamo membro a membro le due equazioni ottenute al punto precedente:
        • $ac=(b+k_{1}m)(d+k_{2}m)$
     3. Sviluppiamo il prodotto: Svolgendo i calcoli otteniamo:
        • $ac=bd+b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2$
        • $ac-bd=b{k}_{2}m+d{k}_{1}m+k_1{k}_2{m}^2$
     4. Evidenziamo m: Mettiamo in evidenza m a secondo membro:
        • $ac-bd=m(b{k}_2+d{k}_1+k_1{k}_{2}m)$
     5. Cosa significa questo risultato?
        • Abbiamo dimostrato che la differenza tra $ac$ e $bd$ è un multiplo di $m$. Quindi, per definizione di congruenza modulo $m$, si ha: $ac\equiv bd(\mathrm{mod}m)$

Questo teorema ha dei casi particolari:

• Invarianza rispetto alla somma: Se sommiamo ad entrambi i membri di una congruenza uno stesso numero intero, la congruenza non cambia
  • $a\equiv b(\mathrm{mod}m)$ allora $a+c\equiv b+c(\mathrm{mod}m)$
• Invarianza rispetto al prodotto: Se moltiplichiamo ambo i membri di una congruenza per uno stesso numero intero, la congruenza non cambia.
  • $a\equiv b(\mathrm{mod}m)$ allora $ac\equiv bc(\mathrm{mod}m)$

Come conseguenza di questi 2 casi particolari, dati $a,b,m\in N$ e visto che $a\equiv a\mathrm{mod}m(\mathrm{mod}m)$ e $b\equiv b\mathrm{mod}m(\mathrm{mod}m)$ valgono le seguenti proprietà:

1. $(a+b)$ ≡ $(a\mathrm{mod}m+b\mathrm{mod}m)(\mathrm{mod}m)$ ossia $(a+b)\mathrm{mod}m$ = $(a\mathrm{mod}m+b\mathrm{mod}m)(\mathrm{mod}m$)
2. $(a\times b)$ ≡ $(a\mathrm{mod}m\times b\mathrm{mod}m)(\mathrm{mod}m)$ ossia $(a\times b)\mathrm{mod}m=((a\mathrm{mod}m)(b\mathrm{mod}m))(\mathrm{mod}m)$ Come conseguenze del punto 2 abbiamo:
3. Dati $a,n,m\in N,a^2\equiv (a\mathrm{mod}m{)}^2(\mathrm{mod}m)$
4. Dati $a,b,h,k,m\in N$ allora $a^h\times b^k\equiv (a^h\mathrm{mod}m)\times (b^k\mathrm{mod}m)(\mathrm{mod}m)$ ossia $a^h\times b^k\mathrm{mod}m=(a\mathrm{mod}m{)}^h\times (b\mathrm{mod}m{)}^k\mathrm{mod}m$

• Invarianza rispetto alla somma: Se sottraiamo ad entrambi i membri di una congruenza uno stesso numero intero, la congruenza non cambia
  • $a\equiv b(\mathrm{mod}m)$ allora $a-c\equiv b-c(\mathrm{mod}m)$
• Invarianza rispetto al prodotto: Se dividiamo ambo i membri di una congruenza per uno stesso numero intero, la congruenza potrebbe non valere più.
  • $6\equiv 0(\mathrm{mod}3)$ è vera
  • se dividiamo tutto per 2 diventa $2\not\equiv 0(\mathrm{mod}3)$ che è falsa

Come diretta conseguenza dell’invarianza rispetto alla somma abbiamo il seguente teorema:

• Per ogni $m\in N,m>1$ , prendendo una qualunque sequenza di m interi questa contiene un intero divisibile per m Dimostrazione: Consideriamo allora m interi consecutivi, dove il più piccolo è n, Come abbiamo già dimostrato, le classi di equivalenza della relazione di congruenza modulo m sono $[0{]}_m,[1{]}_m,[2{]}_m,...[m-1{]}_m$ , il nostro numero $n$ si trova in una di queste classi di equivalenza, supponiamo stia nella classe $[i{]}_m$ per $0\le i\le m-1$. Quindi n ≡ i(mod m) ed allora $n+1\equiv i+1(\mathrm{mod}m)$ ovvero $n+1\in [i+1]m$ Dimostrazione cont. Notiamo allora che se $i=0$ ovvero $n\in [0{]}_m$ abbiamo dimostrato il teorema. Se invece $i>0$, visto che $0<i<m$ incrementando $i$ esattamente $m-i$ volte, con $m-i<m$ otteniamo che n + (m − i) ≡ i + (m − i)(mod m) ossia $n+(m-i)\equiv m(\mathrm{mod}m)\equiv 0(\mathrm{mod}m)$. In conclusione, $n+(m-i)$ è il numero multiplo di $m$ nella sequenza di $m$ numeri consecutivi. Esercizi

---

Divisione modulare

Nei numeri razionali esiste il concetto di “inverso” ovvero preso $a\in Q$ e $a\ne$ 0 esiste un $x\in Q$ tale che $a\ast x=1$, $x$ viene anche denotato con la dicitura $a^{-1}$.

• se $a=2$ allora $a^{-1}=\frac{1}{2}$ Il seguente teorema introduce una nozione simile per l’aritmetica modulare.

Teorema Siano $a,b\in N$ entrambi maggiori di zero. Allora, esiste un elemento $x\in N$ tale che $a\cdot x\equiv 1(\mathrm{mod}b)$ se e solo se $a$ e $b$ sono coprimi. Anche in questo caso l’elemento x viene detto “inverso di a modulo b” e si denota con $a^{-1}$

• con $a=5$, $b=3$ abbiamo che $a^{-1}$ = $2$,
  • infatti $2\cdot 5$ mod $3$ = $10$ mod $3$ = $1$ che è congruo con $1$ mod $3$
• con $a=9$, $b=7$ abbiamo che $a^{-1}$ = $4$,
  • infatti $4\cdot 9$ mod $7$ = $36$ mod $7$ = $1$ che è congruo con $1$ mod $7$

Dimostrazione

---

Funzione di Eulero

Sia $n$ un intero positivo, cioè $n>0$ e vogliamo definire quanti sono i numeri che precedono $n$ e che siano coprimi con $n$, da qui definiamo la funzione detta di Eulero:

• $\varphi (n)=|\{x:x\in \mathbb{N},0<x\le n,MCD(n,x)=1\}|$ La funzione phi di Eulero di n è uguale al numero di numeri naturali x, compresi tra 0 e n (estremi inclusi), tali che il massimo comune divisore tra n e x sia uguale a 1.
  • n = 5 : φ(5) = 4 poiché MCD(5, x) = 1, per x = 1, 2, 3, 4.

Formule generali per il calcolo del $\varphi (n)$ usata negli esercizi

Ci sono delle formule generali per il calcolo del phi di un numero:

1. Se $n$ è un numero primo tutti i predecessori di n sono ad esso coprimi quindi $\varphi (n)=n-1$

   • φ(5) = 4
   • φ(11) = 10

2. Il caso $n$ potenza di numero primo, ovvero $n=p^k$ dove $k\ge 2$ e $p$ è primo, tutti i divisori di $n$ vanno da $p^1,p^2,\dots ,p^k$ e i multipli di $p$ sono $p,2p,3p,\dots ,p^{k-1}$ i multipli di $p$ sono i numeri non coprimi con $n$, quindi facendo la differenza tra $p^k$ e $p^{k-1}$ otteniamo tutti i numeri coprimi con n ovvero $\phi (n)=\phi (p^k)=n-p^{k-1}=p^k-p^{k-1}$

   • φ(8) = φ($2^3$) = $2^3$ − $2^2$ = 8 − 4 = 4
   • φ(27) = φ($3^3$) = $3^3$ − $3^2$ = 27 − 9 = 18

3. Analizziamo il caso $n$ prodotto di due numeri distinti, ovvero n = $p_1\ast p_2$ con $p_1,p_2$ entrambi primi. Tra gli interi $1,2,3,...p_1\cdot p_2$ = $n$ ci sono $p_2$ multipli di $p_1$, ossia $p_1$, $2p_1$, $3p_1$, … , $p_2$ · $p_1$ e, analogamente $p_1$ multipli di $p_2$. Tolti i multipli di $p_1$ e di $p_2$ tutti gli altri interi sono ovviamente coprimi con $n$ e quindi φ(n) = n − $p_1$ − $p_2$ + 1 = $p_1{p}_2$ − $p_1$ − $p_2$ + 1 = ($p_1$ − 1) · ($p_2$ − 1)

   • φ(2 · 3) = (2-1) · (3-1) = 2
   • φ(3 · 5) = (3-1) · (5-1) = 8

Il caso numero 3 può essere generalizzato nel seguente modo: Sia $n=h\cdot k$ dove $h$ e $k$ sono interi maggiori di zero e coprimi tra di loro. Allora $\phi (n)=\phi (h)\cdot \phi (k)$

• φ(4 · 9) = φ($2^2$) · φ($3^2$) = 2 · 6 = 12
• φ(5 · 8) = φ($5$) · φ($2^3$) = 4 · 4 = 16

Formula generale per il calcolo della funzione di Eulero

Utilizzando il teorema di fattorizzazione degli interi possiamo ricavare la formula generale per il calcolo della funzione φ di Eulero. Sia n > 1, consideriamo la sua fattorizzazione $n=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_m^{k_m}$ Allora

• $\varphi (n)=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_m^{k_m}-p_m^{k_m-1})$

Dimostrazione: dimostriamo il teorema per induzione sul numero dei fattori primi presenti nella fattorizzazione di n. Caso base: se $m=1$ allora $p_1^{k_1}$ sappiamo che è vera per il caso 2 Passo induttivo: Supponiamo il teorema sia vero per ogni intero $n^{\prime }$ la cui fattorizzazione presenta $m-1$ primi diversi campiamo che $n^{\prime }=p_1^{k_1}\cdot p_2^{k_2}\cdot ...\cdot p_{m-1}^{k_{m-1}}$ a questo punto la fattorizzazione per $m$ sarà uguale a:

• $n=n\prime \cdot p_m^{k_m}$ dal teorema abbiamo che: $\varphi (n^{\prime })=(p_1^{k_1}-p_1^{k_1-1})\cdot (p_2^{k_2}-p_2^{k_2-1})\cdot \dots \cdot (p_{m-1}^{k_{m-1}}-p_{m-1}^{k_{m-1}-1})$ e quindi $\varphi (n)=\varphi (n^{\prime })\ast (p_m^{k_m}-p_m^{k_m-1})$.

Come possiamo notare il teorema vale sia nel caso base, sia nel passo induttivo e quindi il teorema è dimostrato.

• $\phi (42):42=(2^1-2^{1-1})\cdot (3^1-3^{1-1})\cdot (7^1-7^{1-1})=(2^1-2^0)\cdot (3^1-3^0)\cdot (7^1-7^0)$ Quindi $\phi (42)=1\cdot 2\cdot 6=12$. (in questo esempio ho preferito specificare ogni singolo esponente per renderlo più semplice da capire)

---

Teorema di Eulero

Il seguente teorema, detto Teorema di Eulero, dimostra come la funzione φ di Eulero si possa applicare alla esponenziazione modulare. Siano $n,m$ > $0$, se $MCD(n,m)=1$ allora $n^{\phi (m)}\equiv 1(\mathrm{mod}m)$

• $n=12,m=5:12^4\equiv 1(\mathrm{mod}5)$ infatti $12^4=20736$ e $20736\mathrm{mod}5=1$.

Per dimostrare questo teorema dobbiamo enunciare e dimostrare 2 lemmi

Lemma 1:

Sia $m>1$ e sia $C_m$ = $\{x:0<x<m,MCD(x,m)=1\}$ cioè l’insieme dei numeri interi positivi minori di $m$ e coprimi con $m$. Allora

• a) per ogni $x\in C_m$ esiste $y\in C_m$ tale $x\ast y\equiv 1(\mathrm{mod}m)$
• b) $C_m^{-1}$ = $\{x^{-1}\mathrm{mod}m:x\in C_m\}=C_m$

Dimostrazione:

Punto (a): Dimostrare che ogni elemento di $C_m$ ha un inverso moltiplicativo modulo $m$ che appartiene a $C_m$.

1. Concetto chiave Grazie al teorema di esistenza dell’inverso moltiplicativo, sappiamo che ogni $x\in C_m$ ha un inverso $y$ tale che: $x\cdot y\equiv 1(\mathrm{mod}m).$ Bisogna verificare che $y\in C_m$, cioè che $y$ sia coprimo con $m$.
2. Proprietà utilizzate
   • Dalla definizione di $C_m$, $x$ è coprimo con $m$, quindi: $\text{MCD}(x,m)=1.$
   • La proprietà fondamentale dell’inverso moltiplicativo ci garantisce che: $(x\cdot y)\mathrm{mod}m=1.$
3. Verifica che $y$ è coprimo con $m$:
   • Per definizione, se $x\cdot y\equiv 1(\mathrm{mod}m)$, allora $y$ non può avere un divisore comune con $m$ diverso da 1 (altrimenti $x\cdot y$ non sarebbe congruo a 1 modulo $m$).
   • Quindi $\text{MCD}(y,m)=1$, e quindi $y\in C_m$.

Punto (b): Dimostrare che $C_m^{-1}=C_m$.

1. Definizione di $C_m^{-1}$: $C_m^{-1}$ è l’insieme di tutti gli inversi moltiplicativi modulo $m$ degli elementi di $C_m$.

2. Inclusione $C_m^{-1}\subseteq C_m$: Dal punto (a), sappiamo che ogni elemento di $C_m$ ha un inverso modulo $m$ che appartiene a $C_m$. Questo implica che ogni elemento di $C_m^{-1}$ è un elemento di $C_m$.

3. Inclusione $C_m\subseteq C_m^{-1}$: Ogni $x\in C_m$ ha un inverso $y\in C_m$, ma possiamo considerare $y$ a sua volta come un elemento di $C_m$. Siccome l’operazione di inversione è biunivoca (ovvero ogni elemento ha un singolo inverso), ogni elemento di $C_m$ corrisponde a un elemento di $C_m^{-1}$.

4. Conclusione: Poiché $C_m^{-1}\subseteq C_m$ e $C_m\subseteq C_m^{-1}$, possiamo affermare che: $C_m^{-1}=C_m.$

Esempio: Per $m=10$ abbiamo $C_{10}=\{1,3,7,9\}$ e quindi che:

• $1^{-1}\mathrm{mod}10=1$,
• $3^{-1}\mathrm{mod}10=7,$
• $7^{-1}\mathrm{mod}10=3,$
• $9^{-1}\mathrm{mod}10=9$. Da questo concludiamo che $C_{10}^{-1}$ =$\{1,7,3,9\}$

Lemma 2

Siano $n,m>1$, tale che $MCD(n,m)=1$. Sia $C_{n,m}$ = $\{(n\cdot x)\mathrm{mod}m:x\in C_m\}$. Allora, $C_{n,m}=C_m$

Dimostrazione:

Per dimostrare che $C_{n,m}=C_m$, si procede in due passi:

1. Dimostrare che $C_{n,m}\subseteq C_m$.
2. Dimostrare che $C_m\subseteq C_{n,m}$.

---

1. Primo passo: $C_{n,m}\subseteq C_m$

Dimostriamo che ogni elemento di $C_{n,m}$ appartiene a $C_m$.

1. Prendiamo un $k\in C_{n,m}$. Per definizione di $C_{n,m}$, esiste un $x\in C_m$ tale che:
   $k=(n\cdot x)\mathrm{mod}m$ con $0\le k<m$.
2. Supponiamo, per assurdo, che $k=0$. Allora avremmo:
   $n\cdot x=q\cdot m$ cioè $m$ dividerebbe $n\cdot x$. Ma poiché $\text{MCD}(n,m)=1$, $m$ non può dividere né $n$ né $x$, portando a una contraddizione.
3. Ne consegue che $k>0$. Dato che $x\in C_m$, esiste l’inverso di $x$ modulo $m$, cioè un $x^{-1}$ tale che: $x\cdot x^{-1}\equiv 1(\mathrm{mod}m).$
4. Inoltre, poiché $\text{MCD}(n,m)=1$, anche $n$ ha un inverso modulo $m$, chiamiamolo $n^{-1}$. Allora possiamo calcolare: $k\cdot n^{-1}\equiv x(\mathrm{mod}m).$
5. Dato che $x\in C_m$, abbiamo che $x$ è coprimo con $m$. Questo implica che anche $k$, essendo congruente a $x$, è coprimo con $m$. Quindi: $k\in C_m.$

---

2. Secondo passo: $C_m\subseteq C_{n,m}$

Dimostriamo ora che ogni elemento di $C_m$ appartiene a $C_{n,m}$.

1. Sia $x\in C_m$. Questo implica che $x$ è coprimo con $m$.
2. Poiché $\text{MCD}(n,m)=1$, l’intero $n^{-1}\cdot x$ modulo $m$ esiste. Chiamiamolo $k$, ovvero:
   $k=(n^{-1}\cdot x)\mathrm{mod}m.$
3. Possiamo riscrivere $x$ in termini di $k$: $x=(n\cdot k)\mathrm{mod}m.$
4. Da questa relazione, vediamo che $k\in C_{n,m}$, perché $k$ è costruito come $n\cdot x\mathrm{mod}m$, con $x\in C_m$.
5. Dunque $x\in C_m⟹x\in C_{n,m}$. Conclusione: Poiché abbiamo dimostrato sia $C_{n,m}\subseteq C_m$ sia $C_m\subseteq C_{n,m}$, possiamo concludere che:
   $C_{n,m}=C_m.$

Esempio: Per $m=5$ e $n=13$ abbiamo che MCD(13,5) = 1, inoltre $C_5$ = $\{1,2,3,4\}$ applicando la regola otteniamo $C_{13,5}=\{1\ast 13\mathrm{mod}5,2\ast 13\mathrm{mod}5,3\ast 13\mathrm{mod}5,4\ast 13\mathrm{mod}5\}$, risolviamo i moduli:

• $1\cdot 13\mathrm{mod}5$ = $13\mathrm{mod}5$ = $3$
• $2\cdot 13\mathrm{mod}5$ = $26\mathrm{mod}5$ = $1$
• $3\cdot 13\mathrm{mod}5$ = $39\mathrm{mod}5$ = $4$
• $4\cdot 13\mathrm{mod}5$ = $52\mathrm{mod}5$ = $2$ Quindi $C_{13,5}=3,1,4,2$

Continuare con le slide da 122 fino a 135

---

Applicazioni dell'aritmetica modulare

La prova del 9

La prova del nove è una verifica di correttezza del risultato di una operazione aritmetica tra numeri interi, ricordando la definizione di radice numerica questo è il teorema che definisce la prova del 9: Teorema: dati $n,m\in N$ abbiamo che:

• $\rho (n\ast m)=\rho (\rho (n)\ast p(m))$
• $\rho (n+m)=\rho (\rho (n)+p(m))$ Esempio: $123\ast 347==42671?$ per verificare che è giusto facciamo così:
• $\rho (123)=6$
• $\rho (347)=5$
• $\rho (\rho (123)\ast \rho (347))=\rho (30)=3$
• $\rho (42671)=\rho (20)=2$ Gli ultimi 2 risultati sono sbagliati quindi la moltiplicazione è stata fatta nel modo errato (il vero risultato di $123\ast 347$ è $42681$)

Teorema: dato $n\in N$ abbiamo che:

• $n\equiv \rho (n)(\mathrm{mod}9)$ la radice numeri di un qualsiasi numero è congrua modulo $9$.

Dimostrazione: per il Teorema di divisibilità del $9$ sappiamo che dato $n\in N$, se $m$ è la somma delle sue cifre allora $n-m$ è divisibile per $9$, ossia esiste un $k$ tale che $n-m=9k$. Quindi, ottengo che $n\equiv m(\mathrm{mod}9)$. Reiterando, se $m\prime$ è la somma delle cifre di $m$ otteniamo $m\equiv m\prime (\mathrm{mod}9)$ quindi $n\equiv m(\mathrm{mod}9)\equiv m\prime (\mathrm{mod}9)$. Fermiamo il processo di somma delle cifre quando otteniamo un numero con una sola cifra (ovvero la radice numeri di $n$) quindi concludiamo che $n\equiv \rho (n)(\mathrm{mod}9)$

• $250\equiv 7\mathrm{mod}9$ infatti
  • $250\mathrm{mod}9=7$
  • $7\mathrm{mod}9=7$